题目内容
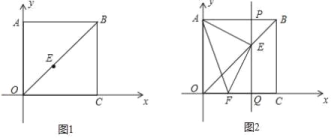
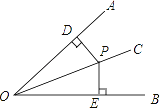
【题目】如图,线段AB的长为10cm,点D是AB上的一个动点,不与点A重合,以AD为边作等边△ACD,过点D作DP⊥CD,过DP上一动点G(不与点D重合)作矩形CDGH,对角线交于点O,连接OA、OB,则线段OB的最小值是________.

【答案】5
【解析】
根据矩形对角线相等且互相平分得:OC=OD,再证明△ACO≌△ADO,则∠OAB=30°;点O一定在∠CAB的平分线上运动,根据垂线段最短得:当OB⊥AO时,OB的长最小,根据直角三角形30度角所对的直角边是斜边的一半得出结论.
解,∵四边形CDGH是矩形,
∴CG=DH,OC=![]() CG,OD=
CG,OD=![]() DH,
DH,
∴OC=OD,
∵△ACD是等边三角形,
∴AC=AD,∠CAD=60°,
∵OA=OA,
∴△ACO≌△ADO,
∴∠OAB=∠CAO=![]() ×60°=30°,
×60°=30°,
∴点O一定在∠CAB的平分线上运动,所以当OB⊥AO时,OB的长最小,
∵∠OAB=30°,∠AOB=90°,
∴OB=![]() AB=
AB=![]() ×10=5,即OB的最小值为5cm,
×10=5,即OB的最小值为5cm,
故答案为:5.

练习册系列答案
相关题目