题目内容
【题目】我们规定:横、纵坐标相等的点叫做“完美点”.
(1)若点A(x,y)是“完美点”,且满足x+y=4,求点A的坐标;
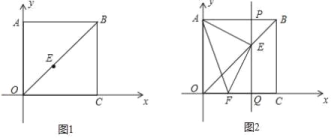
(2)如图1,在平面直角坐标系中,四边形OABC是正方形,点A坐标为(0,4),连接OB,E点从O向B运动,速度为2个单位/秒,到B点时运动停止,设运动时间为t.
①不管t为何值,E点总是“完美点”;
②如图2,连接AE,过E点作PQ⊥x轴分别交AB、OC于P、Q两点,过点E作EF⊥AE交x轴于点F,问:当E点运动时,四边形AFQP的面积是否发生变化?若不改变,求出面积的值;若改变,请说明理由.
【答案】(1)A(2,2);(2)①证明见解析;②当E点运动时,四边形AFQP的面积不变,面积为8.
【解析】
(1)根据“完美点”定义可求点A坐标;(2)①由题意可求直线OB的解析式y=x,点E在直线OB上移动,则可证结论;②根据题意可证△EFQ≌△APE,可求PE=FQ,则可求四边形AFQP的面积.
解(1)∵点A(x,y)是“完美点”
∴x=y
∵x+y=4
∴x=2,y=2
∴A点坐标(2,2)
(2)①∵四边形OABC是正方形,点A坐标为(0,4),
∴AO=AB=BC=4∴B(4,4)
设直线OB解析式y=kx过B点
∴4=4k,k=1
∴直线OB解析式y=x
设点E坐标(x,y)
∵点E在直线OB上移动
∴x=y
∴不管t为何值,E点总是“完美点”.
②∵E点总是“完美点”.
∴EQ=OQ
∵∠BAO=∠AOC=90°,PQ⊥x轴
∴四边形AOQP是矩形
∴AP=OQ,AO=PQ=4
∴AP=EQ
∵AE⊥EF
∴∠AEP+∠FEQ=90°,∠EAP+∠AEP=90°
∴∠FEQ=∠EAP
∵AP=EQ,∠FEQ=∠EAP,∠APE=∠EQF=90°
∴△APE≌△EFQ
∴PE=FQ
∵S四边形AFQP=![]() =2(PE+EQ)=2×PQ=8
=2(PE+EQ)=2×PQ=8
∴当E点运动时,四边形AFQP的面积不变,面积为8.

 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案