题目内容
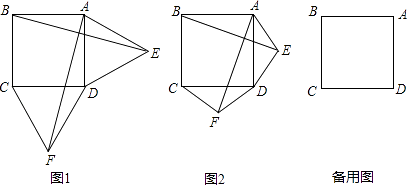
【题目】如图①, ![]() 是
是![]() 的边
的边![]() 上的高,且
上的高,且![]() cm,
cm,![]() cm,点
cm,点![]() 从点
从点![]() 出发,沿线段
出发,沿线段![]() 向终点
向终点![]() 运动,其速度与时间的关系如图②所示,设点
运动,其速度与时间的关系如图②所示,设点![]() 的运动时间为
的运动时间为![]() (s),
(s),![]() 的面积为
的面积为![]() (cm2 ).
(cm2 ).
(1)在点![]() 沿
沿![]() 向点
向点![]() 运动的过程中,它的速度是 cm/s,用含
运动的过程中,它的速度是 cm/s,用含![]() 的代数式表示线段
的代数式表示线段![]() 的长是 cm,变量
的长是 cm,变量![]() 与
与![]() 之间的函数表达式为;
之间的函数表达式为;
(2)当![]() 时,求
时,求![]() 的值.当
的值.当![]() 每增加1时,求
每增加1时,求![]() 的变化情况.
的变化情况.

【答案】(1)3cm/s, ![]() 的长是
的长是![]() cm,
cm,![]() ;(2)
;(2) ![]() =24.当
=24.当![]() 每增加1时,
每增加1时,![]() 增加12.
增加12.
【解析】
(1)根据图2即可求得点E沿BC向点C运动的过程中的速度,根据速度、路程和时间的关系即可求得BE的长,进而根据三角形面积公式求得y与x的关系式;
(2)把x=2代入关系式即可求得y的值,直线的斜率就是函数的变化率.
解:

(1)由图2可知,在点E沿BC向点C运动的过程中,它的速度是3cm/s,
所以线段BE的长是3xcm;
根据三角形的面积公式得:y=![]() ×3x×8=12x;
×3x×8=12x;
(2)当x=2时,y=12×2=24;
由y=12x可知,因为12是斜率,说明x每增加一个单位,y增加12个单位,
所以当x每增加1s时,y增加12cm2,
故答案为: (1)3cm/s; ![]() 的长是
的长是![]() cm;
cm; ![]() ;(2)
;(2) ![]() =24;当
=24;当![]() 每增加1时,
每增加1时,![]() 增加12.
增加12.
.

练习册系列答案
相关题目