题目内容
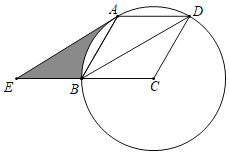
【题目】如图,在![]() 中,
中,![]() ,以
,以![]() 为直径的
为直径的![]() 与边
与边![]() ,
,![]() 分别交于
分别交于![]() ,
,![]() 两点,过点
两点,过点![]() 作
作![]() 于点
于点![]() .
.
(1)判断![]() 与
与![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
(2)求证:![]() 为
为![]() 的中点;
的中点;
(3)若![]() ,
,![]() ,求
,求![]() 的长.
的长.
【答案】(1)![]() 与
与![]() 相切,理由见解析;(2)详见解析;(3)
相切,理由见解析;(2)详见解析;(3)![]() .
.
【解析】
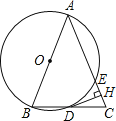
(1)连结![]() 、
、![]() ,如图1,先利用AB是圆的直径得到
,如图1,先利用AB是圆的直径得到![]() ,再根据等腰三角形的性质得
,再根据等腰三角形的性质得![]() ,然后利用三角形中位线定理可得
,然后利用三角形中位线定理可得![]() ,而
,而![]() ,进一步即可证得结论;
,进一步即可证得结论;
(2)连结![]() ,如图2,根据圆内接四边形的性质和等腰三角形的性质可得
,如图2,根据圆内接四边形的性质和等腰三角形的性质可得![]() ,从而DE=DC,然后根据等腰三角形三线合一的性质即可证得结论;
,从而DE=DC,然后根据等腰三角形三线合一的性质即可证得结论;
(3)易得![]() ,利用余弦的定义,分别在
,利用余弦的定义,分别在![]() 和
和![]() 中计算出AC与CH的长,则CE即可求出,然后计算
中计算出AC与CH的长,则CE即可求出,然后计算![]() 即可得到
即可得到![]() 的长.
的长.
解:(1)![]() 与
与![]() 相切.理由如下:
相切.理由如下:
连结![]() 、
、![]() ,如图1,∵
,如图1,∵![]() 为直径,∴
为直径,∴![]() ,即
,即![]() ,
,
∵![]() ,∴
,∴![]() ,
,
而![]() ,∴
,∴![]() 为
为![]() 的中位线,∴
的中位线,∴![]() ,
,
∵![]() ,∴
,∴![]() ,∴
,∴![]() 为
为![]() 的切线;
的切线;
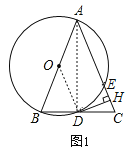
(2)证明:连结![]() ,如图2,
,如图2,
∵四边形![]() 为
为![]() 的内接四边形,∴
的内接四边形,∴![]() ,
,
∵![]() ,∴
,∴![]() ,∴
,∴![]() ,∴DE=DC.
,∴DE=DC.
∵![]() ,∴
,∴![]() ,即
,即![]() 为
为![]() 的中点;
的中点;
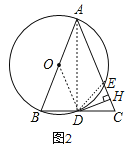
(3)解:如图2,在![]() 中,∵
中,∵![]() ,
,![]() ,∴
,∴![]() .
.
在![]() 中,∵
中,∵![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∴![]()
![]() .
.

【题目】4月23日是世界读书日,校文学社为了解学生课外阅读的情况,抽样调查了部分学生每周用于课外阅读的时间,过程如下:
收集数据:从学校随机抽取20名,进行了每周用于课外阅读时间的调查,数据如下(单位:![]() ):
):
30 | 60 | 81 | 50 | 40 | 110 | 130 | 146 | 90 | 100 |
60 | 81 | 120 | 140 | 70 | 81 | 10 | 20 | 100 | 81 |
整理数据:按如下分数段整理样本数据并补全表格:
|
|
|
| |
等级 |
|
|
|
|
人数 | 3 |
| 8 | 4 |
分析数据:补全下列表格中的统计量:
平均数 | 中位数 | 众数 |
80 |
|
|
得出结论:
(1)请写出表中![]() _________;
_________;![]() _________
_________![]() ;
;![]() __________
__________![]() ;
;
(2)如果该校现有学生7500人,估计等级为“![]() ”的学生有_________名;
”的学生有_________名;
(3)假设平均阅读一本课外书的时间为![]() ,请你选择一种统计量估计该校学生每人一年(按52周计算)平均阅读多少本课外书?
,请你选择一种统计量估计该校学生每人一年(按52周计算)平均阅读多少本课外书?
【题目】已知蓄电池的电压为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:![]() )是反比例函数关系.当
)是反比例函数关系.当![]() 时,
时,![]() .
.
(1)写出I关于R的函数解析式;
(2)完成下表,并在给定的平面直角坐标系中画出这个函数的图象;
| … | … | ||||||||
| … | … |
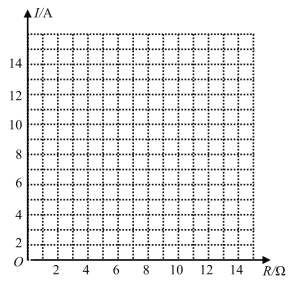
(3)如果以此蓄电池为电源的用电器的限制电流不能超过![]() .那么用电器可变电阻应控制在什么范围内?
.那么用电器可变电阻应控制在什么范围内?