题目内容
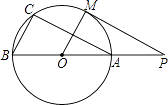
【题目】如图,AB为⊙O的直径,AC交⊙O于E点,BC交⊙O于D点,CD=BD,∠C=70°.现给出以下四种结论:①∠A=45°;②AC=AB;③AE=BE;④CEAB=2BD2 . 其中正确结论的序号是( ) 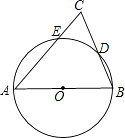
A.①②
B.②③
C.②④
D.③④
【答案】C
【解析】解:连接AD,
∵AB是⊙O的直径,
∴∠ADB=90°.
∵CD=BD,
∴AD是BC的垂直平分线,
∴AC=AB,故②正确;
∵AC=AB,
∴∠ABC=∠C=70°,
∴∠BAC=40°,故①错误;
连接BE,DE,
∵AB为⊙O的直径,
∴∠AEB=90°,
∵∠BAC=40°,
∴∠ABE=50°,
∴∠BAC≠∠ABE,
∴AE≠BE,故③错误;
∵四边形ABDE是圆内接四边形,
∴∠CDE=∠CAB,
∴△CDE∽△CAB,
∴ ![]() =
= ![]() ,即
,即 ![]() ,
,
∴CEAB=2BD2 , 故④正确.
故选C.
【考点精析】通过灵活运用相似三角形的判定与性质,掌握相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方即可以解答此题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目