题目内容
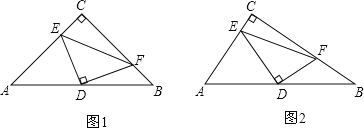
【题目】如图,在△ABC中,AD⊥BC于D,AE平分∠BAC.
(1)若∠B=70°,∠C=40°,求∠DAE的度数.
(2)若∠B﹣∠C=30°,则∠DAE= .
(3)若∠B﹣∠C=α(∠B>∠C),求∠DAE的度数(用含α的代数式表示)

【答案】(1)15°;(2)15°;(3)![]() α;
α;
【解析】
(1)根据角平分线的定义和互余进行计算;
(2)根据三角形内角和定理和角平分线定义得出∠DAE的度数等于∠B与∠C差的一半解答即可;
(3)根据(2)中所得解答即可.
解:∵AD⊥BC于D,
∴∠ADC=90°,
∵AE平分∠BAC,
∴∠EAC=![]() ∠BAC,
∠BAC,
而∠BAC=180°﹣∠B﹣∠C,
∴∠EAC=90°﹣![]() ∠B﹣
∠B﹣![]() ∠C,
∠C,
∵∠DAC=90°﹣∠C,
∴∠DAE=∠DAC﹣∠EAC=90°﹣∠C﹣[90°﹣![]() ∠B﹣
∠B﹣![]() ∠C]
∠C]
=![]() (∠B﹣∠C),
(∠B﹣∠C),
(1)若∠B=70°,∠C=40°,则∠DAE=![]() (70°﹣40°)=15°;
(70°﹣40°)=15°;
(2)若∠B﹣∠C=30°,则∠DAE=![]() ×30°=15°;
×30°=15°;
(3)若∠B﹣∠C=α(∠B>∠C),则∠DAE=![]() α;
α;

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
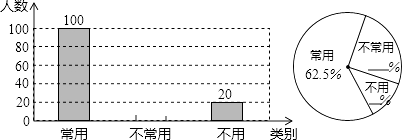
【题目】某校课外兴趣小组在本校学生中开展“感动中国2016年度人物”先进事迹知晓情况专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为A,B,C,D四类,其中,A类表示“非常了解”,B类表示“比较了解”,C类表示“基本了解”,D类表示“不太了解”,划分类别后的数据整理如下表:
类别 | A | B | C | D |
频数 | 30 | 40 | 24 | b |
频率 | a | 0.4 | 0.24 | 0.06 |

(1)表中的a= , b=;
(2)根据表中数据,求扇形统计图中类别为B的学生数所对应的扇形圆心角的度数;
(3)若该校有学生1000名,根据调查结果估计该校学生中类别为D的人数约为多少?