Question

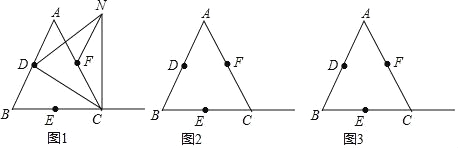
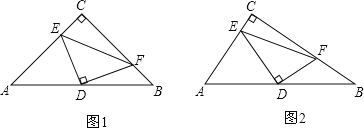
【题目】已知：如图1，Rt△ABC中，∠ACB=90°，D为AB中点，DE、DF分别交AC于E，交BC于F，且DE⊥DF．

（1）如果CA=CB，求证：AE2+BF2=EF2；

（2）如图2，如果CA＜CB，（1）中结论还能成立吗？若成立，请证明；若不成立，请说明理由．

Answer 1

【答案】（1）证明见解析；（2）答案见解析

【解析】

（1）过点A作AM∥BC，交FD延长线于点M，连接EM，通过证明AM=BF，EF=EM即可得出答案；（2）延长FD至M，使DM=DF，连接AM、EM，根据（1）通过证明AM=BF，EF=EM即可得出答案．

解答：

（1）证明：过点A作AM∥BC，交FD延长线于点M，（或将△FBD旋转180°）

连接EM．

∵AM∥BC，

∴∠MAE=∠ACB=90°，∠MAD=∠B．

∵AD=BD，∠ADM=∠BDF，

∴△ADM≌△BDF．

∴AM=BF，MD=DF．

又DE⊥DF，∴EF=EM．

∴AE2+BF2=AE2+AM2=EM2=EF2．

（2）成立．
证明：延长FD至M，使DM=DF，连接AM、EM．
∵AD=BD，∠ADM=∠BDF，
∴△ADM≌△BDF．
∴AM=BF，∠MAD=∠B．
∴AM∥BC．∴∠MAE=∠ACB=90°．
又DE⊥DF，MD=FD，∴EF=EM．
∴AE2+BF2=AE2+AM2=EM2=EF2