题目内容
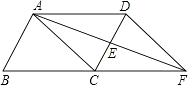
【题目】如图，△ABC为等腰直角三角形，点D是边BC上一动点，以AD为直角边作等腰直角△ADE，分别过A、E点向BC边作垂线，垂足分别为F、G．连接BE．
（1）证明：BG=FD；
（2）求∠ABE的度数．
【答案】(1)见解析;(2) 90°.
【解析】
（1）根据等腰直角三角形的性质得到AD=DE，∠ADE=90°，根据余角的性质得到∠FAD=∠GDE，根据全等三角形的性质得到DG=AF，根据等腰直角三角形的性质得到AF=BF，于是得到结论；
（2）根据等腰直角三角形的性质得到∠ABC=45°，根据全等三角形的性质得到DF=EG，推出△BGE是等腰直角三角形，于是得到结论．
（1）∵△ADE为等腰直角三角形，
∴AD=DE，∠ADE=90°，
∵AF⊥BC，EG⊥BC，
∴∠AFD=∠DGE=90°，
∴∠DAF+∠ADF=∠ADF+∠EDG=90°，
∴∠FAD=∠GDE，
在△ADF与△DEG中，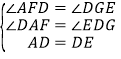
，
∴△ADF≌△DEG，
∴DG=AF，
∵△ABC是等腰直角三角形，
∴AF=BF，
∴BF=DG，
∴BG=DF；
（2）∵△ABC是等腰直角三角形，
∴∠ABC=45°，
∵△ADF≌△DEG，
∴DF=EG，
∴BG=EG，
∵BG⊥EG，
∴△BGE是等腰直角三角形，
∴∠GBE=45°，
∴∠ABE=90°．
激活思维优加课堂系列答案
活力试卷系列答案
课课优能力培优100分系列答案
【题目】某公司需招聘一名员工，对应聘者甲、乙、丙从笔试、面试、体能三个方面进行量化考核．甲、乙、丙各项得分如下表：
笔 试 | 面 试 | 体 能 | |
甲 | 85 | 80 | 75 |
乙 | 80 | 90 | 73 |
丙 | 83 | 79 | 90 |
（1）根据三项得分的平均分，从高到低确定三名应聘者的排名顺序．
（2）该公司规定：笔试，面试、体能得分分别不得低于80分，80分，70分，并按60%，30%，10%的比例计入总分（不计其他因素条件），请你说明谁将被录用．
【题目】虽然近几年无锡市政府加大了太湖水治污力度，但由于大规模、高强度的经济活动和日益增加的污染负荷，使部分太湖水域水质恶化，富营养化不断加剧．为了保护水资源，我市制定一套节水的管理措施，其中对居民生活用水收费作如下规定：
月用水量（吨） | 单价（元/吨） |
不大于10吨部分 | 1.5 |
大于10吨不大于m吨部分（20≤m≤50） | 2 |
大于m吨部分 | 3 |
（1）若某用户六月份用水量为18吨，求其应缴纳的水费；
（2）记该用户六月份用水量为x吨，缴纳水费为y元，试列出y关于x的函数关系式；
（3）若该用户六月份用水量为40吨，缴纳水费y元的取值范围为70≤y≤90，试求m的取值范围．
