题目内容
【题目】解下列各题
（1）解方程： 
=1﹣ 
（2）解不等式组： 
．
【答案】
（1）解：去分母得2﹣x=x﹣3+1，
解得x=2，
检验：当x=2时，x﹣3≠0，
所以原方程的解为x=2
（2）解：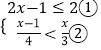 
，
∵解①得x≤ 
，
解②得x＞﹣3，
∴﹣3＜x≤
【解析】（1）方程两边都乘以x﹣3得2﹣x=x﹣3+1，解得x=2，然后进行检验确定分式方程的解；（2）分别解两个不等式得到x≤ 和x＞﹣3，然后根据大于小的小于大的取中间得到不等式组的解．
【考点精析】认真审题，首先需要了解去分母法(先约后乘公分母，整式方程转化出．特殊情况可换元，去掉分母是出路．求得解后要验根，原留增舍别含糊)，还要掌握一元一次不等式组的解法(解法：①分别求出这个不等式组中各个不等式的解集；②利用数轴表示出各个不等式的解集；③找出公共部分；④用不等式表示出这个不等式组的解集．如果这些不等式的解集的没有公共部分，则这个不等式组无解 ( 此时也称这个不等式组的解集为空集 ))的相关知识才是答题的关键．
练习册系列答案
相关题目
【题目】某公司需招聘一名员工，对应聘者甲、乙、丙从笔试、面试、体能三个方面进行量化考核．甲、乙、丙各项得分如下表：
笔 试 | 面 试 | 体 能 | |
甲 | 85 | 80 | 75 |
乙 | 80 | 90 | 73 |
丙 | 83 | 79 | 90 |
（1）根据三项得分的平均分，从高到低确定三名应聘者的排名顺序．
（2）该公司规定：笔试，面试、体能得分分别不得低于80分，80分，70分，并按60%，30%，10%的比例计入总分（不计其他因素条件），请你说明谁将被录用．
