题目内容
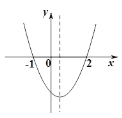
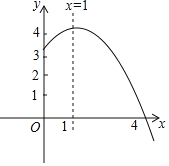
【题目】已知抛物线![]() 与
与![]() 轴、
轴、![]() 轴分别相交于点A(-1,0)和B(0,3),其顶点为D。
轴分别相交于点A(-1,0)和B(0,3),其顶点为D。
(1)求这条抛物线的解析式;
(2)画出此抛物线;
(3)若抛物线与![]() 轴的另一个交点为E,求△ODE的面积;
轴的另一个交点为E,求△ODE的面积;
(4)抛物线的对称轴上是否存在点P使得△PAB的周长最短。若存在请求出点P的坐标,若不存在,说明理由.
【答案】(1)y=﹣x2+2x+3 ;(2)如图所示,见解析;(3)S△ODE=6;(4)存在,点P坐标(1,2).
【解析】
(1)将点A、B的坐标代入![]() 求出b,c即可;
求出b,c即可;
(2)描点、画图即可;
(3)令y=0求出x的值,可得E点坐标,把抛物线一般式化成顶点式可得顶点D的坐标,然后根据三角形面积公式计算即可;
(4)连接BE交抛物线的对称轴x=1于点P,此时PA+PB的值最小,即△PAB的周长最短,求出直线BE的解析式,然后即可解决问题.
解:(1)根据题意得![]() ,
,
解得![]() ,
,
∴抛物线解析式为y=﹣x2+2x+3;
(2)如图所示:
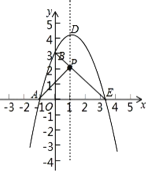
(3)当y=0时,即﹣x2+2x+3=0,
解得:x1=﹣1,x2=3,
∴E(3,0),
∵抛物线y=﹣x2+2x+3=﹣(x﹣1)2 + 4,
∴顶点坐标D(1,4),
∴S△ODE=![]() ×3×4=6;
×3×4=6;
(4)连接BE交抛物线的对称轴x=1于点P,如图,此时PA+PB的值最小,即△PAB的周长最短,
设直线BE的解析式为y=kx+b(k≠0),
则![]() ,解得:
,解得:![]() ,
,
∴直线BE的解析式为:y=﹣x+3,
当x=1时,y=﹣x+3=2,
∴点P坐标为(1,2).

 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案【题目】共享单车逐渐成为市民喜爱的“绿色出行” 方式之一,今年国庆假期某一天,济川中学初三数学社团的同学们随机调查了一个社区,将这天部分出行市民使用共享单车的数据整理成如下统计表.
使用次数 | 0 | 1 | 2 | 3 | 4 | 5 |
人数 | 11 | 15 | 23 | 28 | 18 | 5 |
(1) 这天部分出行市民使用共享单车次数的中位数是__________,众数是__________
(2) 这天部分出行市民平均每人使用共享单车多少次?
(3) 若该社区这天有1500人出行,请你估计这天使用共享单车次数在3次以上(含3 次)的市民有多少人?