题目内容
如图,方格纸中每个小正方形的边长为1,△ABC和△DEF的顶点都在格点上(小正方形的顶点).P1,P2,P3,P4,P5是△DEF边上的5个格点,请在这5个格点中选取2个作为三角形的顶点,使它和点D构成的三角形与△ABC相似,写出所有符合条件的三角形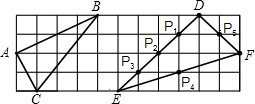
分析:设网格的边长为1,两个三角形的三边对应成比例,那么这两个三角形相似,我们把D点和另外两点连接,三边和△ABC对应成比例的三角形即为所求的三角形.
解答:解:设网格的边长为1.
则AC=
,AB=
,BC=
.
连接DP2P5,
DP5=
,DP2=
,P2P5=
.
∵
=
=
,
∴△ACB∽△DP5P2.
同理可找到△DP2P4,DP4P5和△ACB相似.
故答案为:△DP2P5,DP2P4,DP4P5.
则AC=
| 5 |
| 20 |
| 25 |
连接DP2P5,
DP5=
| 2 |
| 8 |
| 10 |
∵
| ||
|
| ||
|
| ||
|
∴△ACB∽△DP5P2.
同理可找到△DP2P4,DP4P5和△ACB相似.
故答案为:△DP2P5,DP2P4,DP4P5.
点评:本题是在网格型图形中找相似三角三角形,关键是知道相似三角形的判定定理,三边对应成比例,是相似三角形.

练习册系列答案
相关题目
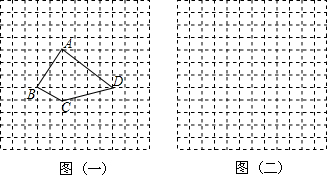
 如图,方格纸中每个小正方形的边长都是单位1.
如图,方格纸中每个小正方形的边长都是单位1.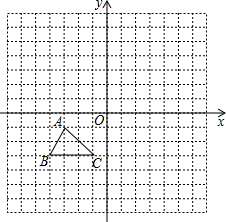 系后,△ABC的顶点在格点上,点B的坐标为(-4.-3).
系后,△ABC的顶点在格点上,点B的坐标为(-4.-3).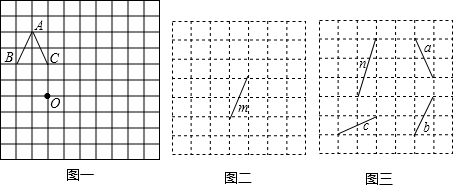
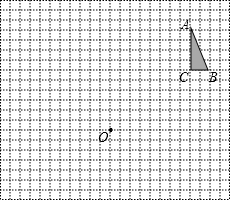
 如图,方格纸中每个小正方形的边长都是单位1,△ABC和点S的位置如图所示.
如图,方格纸中每个小正方形的边长都是单位1,△ABC和点S的位置如图所示.