题目内容
如图,方格纸中每个小方格都是边长为1的正方形,我们把以格点连线为边的多边形称为“格点多边形”,如图1中四边形ABCD就是一个“格点四边形”.(1)求图1中四边形ABCD的面积;
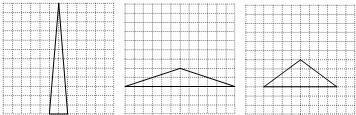
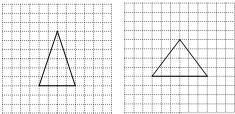
(2)在图2方格纸中画一个格点三角形EFG,使△EFG的面积等于四边形ABCD的面积且为轴对称图形.
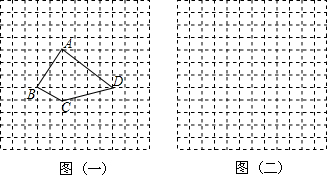
分析:(1)用矩形面积减去周围三角形面积即可;
(2)画一个面积为12的等腰三角形,即底和高相乘为24即可.
(2)画一个面积为12的等腰三角形,即底和高相乘为24即可.
解答:解:(1)根据面积公式得:方法一:S=
×6×4=12;
方法二:S=4×6-
×2×1-
×4×1-
×3×4-
×2×3=12;
(2)(只要画出一种即可)
 (8分)
(8分)
| 1 |
| 2 |
方法二:S=4×6-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(2)(只要画出一种即可)

 (8分)
(8分)点评:解答此题要明确:如果一个图形沿着一条直线对折,直线两侧的图形能够完全重合,这个图形就是轴对称图形;
对称轴:折痕所在的这条直线叫做对称轴.
对称轴:折痕所在的这条直线叫做对称轴.

练习册系列答案
相关题目
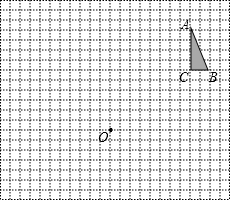 如图,方格纸中每个小正方形的边长都是单位1.
如图,方格纸中每个小正方形的边长都是单位1.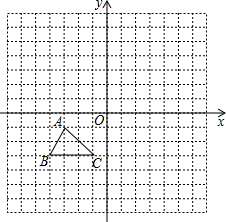 系后,△ABC的顶点在格点上,点B的坐标为(-4.-3).
系后,△ABC的顶点在格点上,点B的坐标为(-4.-3).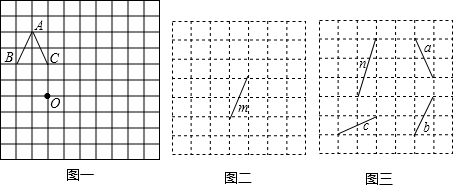
 如图,方格纸中每个小正方形的边长都是单位1,△ABC和点S的位置如图所示.
如图,方格纸中每个小正方形的边长都是单位1,△ABC和点S的位置如图所示.