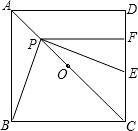
题目内容
边长为4的正方形ABCD中,点O是对角线AC的中点,P是对角线AC上一动点,过点P作PF⊥CD于点F,作PE⊥PB交直线CD于点E,设PA=x,S△PCE=y,
(1)求证:DF=EF;
(2)当点P在线段AO上时,求y关于x的函数关系式及自变量x的取值范围;
(3)在点P的运动过程中,△PEC能否为等腰三角形?如果能够,请直接写出PA的长;如果不能,请简单说明理由.
(1)求证:DF=EF;
(2)当点P在线段AO上时,求y关于x的函数关系式及自变量x的取值范围;
(3)在点P的运动过程中,△PEC能否为等腰三角形?如果能够,请直接写出PA的长;如果不能,请简单说明理由.

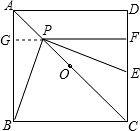
(1)证明:延长FP交AB于G,
∵四边形ABCD是正方形,
∴∠BAD=∠D=90°(正方形的四个内角都是直角)
∵PF⊥CD,
∴∠DFG=90°,
∴四边形AGFD是矩形(有三个角是直角的四边形是矩形),
∴DF=AG,∠AGF=90°,
∵AC是正方形ABCD的对角线,
∴∠BAC=45°,
∴△AGP是等腰直角三角形,即AG=GP,
∴GP=DF,
同理CF=PF=BG,
∵∠GPB+∠FPE=90°,∠GPB+∠GBP=90°,
∴∠GBP=∠FPE,
在Rt△GBP和Rt△FPE中
,
∴Rt△GBP≌Rt△FPE(ASA),
∴GP=EF,
即DF=EF.
(2)在Rt△AGP中,∵AP=x,
∴AG=GP=
x,
DF=EF=
x,
即DE=
x,
∴CE=4-
x,
∵PF=4-
x,
∴y=
(4-
x)(4-
x)=
x2-3
x+8,
定义域:0≤x≤2
,
答:y关于x的函数关系式是y=
x2-3
x+8,自变量x的取值范围是0≤x≤2
.
(3)能够,
∵∠CEP≥90°,
若△PEC为等腰三角形,只能是∠CPE=∠ECP=45°,
则PE⊥CE,
∵PE⊥PB,
∴BP∥CD,
∴BP∥BA
于是P与AB共线,又P在AC上,
∴A与P共点,
此时,PA=0;
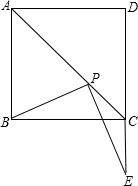
作PE⊥PB交直线CD于点E,
当PA=4时,E在DC的延长线上,PC=CE,
△PEC为等腰三角形,
此时PA=4.
∵四边形ABCD是正方形,
∴∠BAD=∠D=90°(正方形的四个内角都是直角)
∵PF⊥CD,
∴∠DFG=90°,
∴四边形AGFD是矩形(有三个角是直角的四边形是矩形),
∴DF=AG,∠AGF=90°,
∵AC是正方形ABCD的对角线,
∴∠BAC=45°,
∴△AGP是等腰直角三角形,即AG=GP,
∴GP=DF,
同理CF=PF=BG,
∵∠GPB+∠FPE=90°,∠GPB+∠GBP=90°,
∴∠GBP=∠FPE,
在Rt△GBP和Rt△FPE中
|
∴Rt△GBP≌Rt△FPE(ASA),
∴GP=EF,
即DF=EF.
(2)在Rt△AGP中,∵AP=x,
∴AG=GP=
| ||
| 2 |
DF=EF=
| ||
| 2 |
即DE=
| 2 |
∴CE=4-
| 2 |
∵PF=4-
| ||
| 2 |
∴y=
| 1 |
| 2 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| 2 |
定义域:0≤x≤2
| 2 |
答:y关于x的函数关系式是y=
| 1 |
| 2 |
| 2 |
| 2 |
(3)能够,
∵∠CEP≥90°,
若△PEC为等腰三角形,只能是∠CPE=∠ECP=45°,
则PE⊥CE,
∵PE⊥PB,
∴BP∥CD,
∴BP∥BA
于是P与AB共线,又P在AC上,
∴A与P共点,
此时,PA=0;

作PE⊥PB交直线CD于点E,
当PA=4时,E在DC的延长线上,PC=CE,
△PEC为等腰三角形,
此时PA=4.


练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目







