Question

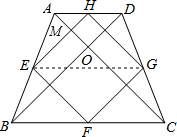
如图，梯形ABCD中，AD∥BC，AB=CD，对角线AC、BD交于点O，AC⊥BD，E、F、G、H分别为AB、BC、CD、DA的中点．
（1）求证：四边形EFGH为正方形；
（2）若AD=1，BC=3，求正方形EFGH的边长．

Answer 1

（1）证明：在△ABC中，
∵E、F分别是AB、BC的中点，
∴EF=

1

2

AC
同理FG=

1

2

BD，GH=

1

2

AC，HE=

1

2

BD
在梯形ABCD中，
∵AB=DC，
∴AC=BD，
∴EF=FG=GH=HE
∴四边形EFGH为菱形．
设AC与EH交于点M
在△ABD中，∵E、H分别是AB、AD的中点，
∴EH∥BD，同理GH∥AC
又∵AC⊥BD，
∴∠BOC=90°．
∴∠EHG=∠EMC=∠BOC=90°
∴四边形EFGH为正方形．

（2）连接EG，在梯形ABCD中，
∵E、G分别是AB、DC的中点，
∴EG=

1

2

（AD+BC）=

1

2

（1+3）=2，
在Rt△HEG中，
EG²=EH²+HG²，
4=2EH²，
EH²=2，
则EH=

2

．
即四边形EFGH的边长为

2

．