题目内容
【题目】为了美化校园，学校决定利用现有的2660盆甲种花卉和3000盆乙种花卉搭配A、B两种园艺造型共50个摆放在校园内，已知搭配一个A种造型需甲种花卉70盆，乙种花卉30盆，搭配一个B种造型需甲种花卉40盆，乙种花卉80盆．则符合要求的搭配方案有几种（ ）
A. 2B. 3C. 4D. 5
【答案】B
【解析】
根据题意列出摆50个A、B园艺所需甲、乙两种花卉各自的总数．令甲的总数小于2660，乙的总数小于3000，联立不等式求出未知量的取值范围，．
设搭配A种造型x个，则B种造型为（50﹣x）个．
依题意，得：
，
解得：
20≤x≤22
∵x是整数，∴x可取20、21、22，
∴可设计三种搭配方案：
①A种园艺造型20个B种园艺造型30个．
②A种园艺造型21个B种园艺造型29个．
③A种园艺造型22个B种园艺造型28个．
故选：B．
练习册系列答案
寒假天地重庆出版社系列答案
相关题目
【题目】今年疫情防控期间，我市一家服装有限公司生产了一款服装，为对比分析以前实体商店和现在网上商店两种途径的销售情况，进行了为期30天的跟踪调查．其中实体商店的日销售量
（百件）与时间
（为整数，单位：天）的部分对应值如下表所示；网上商店的日销售量
（百件）与时间（为整数，单位：天）的关系如图所示．
时间 | 0 | 6 | 10 | 12 | 18 | 20 | 24 | 30 |
日销售量 | 0 | 72 | 100 | 108 | 108 | 100 | 72 | 0 |
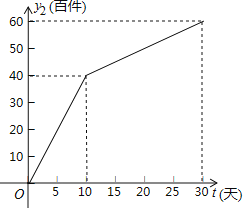
（1）请你在一次函数、二次函数和反比例函数中，选择合适的函数反映与的变化规律，并求出与的函数关系式及自变量的取值范围；
（2）求与的函数关系式，并写出自变量的取值范围；
（3）在跟踪调查的30天中，设实体商店和网上商店的日销售总量为
（百件），求与的函数关系式；当为何值时，日销售量达到最大，并求出此时的最大值．
