Question

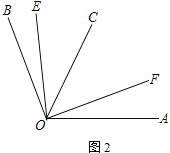
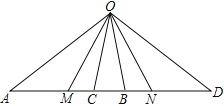
【题目】如图，点O为线段AD外一点，M、C、B、N为AD上任意四点，连接OM、OC、OB、ON，下列结论不正确的是（ ）

A. 以O为顶点的角共有15个

B. 若OM平分∠AOC，ON平分∠BOD，∠AOD＝5∠COB，则∠MON＝(∠MOC＋∠BON)

C. 若M为AB中点，N为CD中点，则MN＝(AD－CB)

D. 若MC＝CB，MN＝ND，则CD＝2CN

Answer 1

【答案】D

【解析】

A.以O为顶点的角的射线一共有6条射线，所以角的个数为6×（6-1）÷2=15个角，由此得出答案即可;

B.根据角平分线的定义和角的和差即可得到结论,根据已知条件列方程即可得到结论;

C. 根据线段的和差，可得MN=MB-CB+CN，根据线段中点的性质，可得MB,CB,CN的关系，再根据线段的和差，可得答案;

D. 由中点可得线段相等，进而可得出线段之间的数量关系．

解：A.6×（6-1）÷2=15个角，故正确；

B. ∵∠AOD＝5∠COB,

∴设∠COB=x°,则∠AOD=5x°,

∴∠AOC+∠BOD=5x°- x°=4x°,

∵OM平分∠AOC，ON平分∠BOD，

∴∠MOC+∠BON=2x°,

∴∠MON=2x°+ x°=3 x°,

∴∠MON＝(∠MOC＋∠BON),

故正确;

C. ∵M为AB中点，N为CD中点，

∴MB=AB,CN=CD,

∴MN=MB-CB+CN

=AB-CB+CD

=(AB+CD)-CB

=(AD+CB-2CD)

=(AD－CB),

故正确;

D. ∵MC＝CB，MN＝ND

∴CD=MD-MC=2MN-MC,

得不出CD＝2CN,

故错误,

故选D.