题目内容
【题目】如图，已知二次函数y=ax2+ 
x+c的图象与y轴交于点A（0，4），与x轴交于点B，C，点C的坐标为（8，0），连接AC．
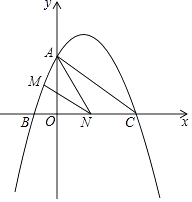
（1）请直接写出二次函数y=ax2+ x+c的表达式；
（2）判断△ABC的形状，并说明理由；
（3）若点N在线段BC上运动（不与点B、C重合），过点N作NM∥AC，交AB于点M，当△AMN面积最大时，求此时N的坐标．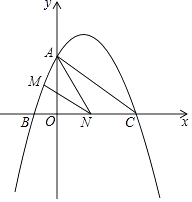
【答案】
（1）
解：将点A和点C的坐标代入得： 
，
解得：a=﹣ 
，c=4．
∴该二次函数的解析式为y=﹣ x2+ 
x+4
（2）
解：令y=0得：﹣ x2+ x+4=0，解得：x=﹣2或x=8，
∴点B（﹣2，0）．
∴BC=10．
在Rt△AOB和Rt△AOC中，依据勾股定理可知：AB2=OB2+AO2=20，AC2=OA2+OC2=80，
∴AB2+AC2=BC2．
∴△ABC为直角三角形
（3）
解：设点N的坐标为（n，0）（﹣2＜n＜8），则BN=n+2，CN=8﹣n．
∵MN∥AC，
∴ 
= 
．
∵AO=4，BC=10，
∴S△ABC= 
BCAO= ×4×10=20．
∴S△ABN= 
S△ABC=2（n+2）．
∴S△AMN= S△AMN= 
（8﹣n）（n+2）=﹣ （n﹣3）2+5．
∴当n=3时，即N（3，0）时，△AMN的面积最大，最大值为5
【解析】（1）将点A和点C的坐标代入代入抛物线的解析式，求得a，c的值即可；（2）先求得点B的坐标，从而得到BC=10，然后依据勾股定理可求得AB2、AC2的值，最后依据勾股定理的逆定理进行判断即可；（3）设点N的坐标为（n，0）（﹣2＜n＜8），则BN=n+2，CN=8﹣n，利用平行线分线段成比例定理可得到 = ，然后依据等高的两个三角形的面积比等于底边的长度比可得到S△AMN与n的函数关系式，最后利用二次函数的性质可求得△AMN的面积取得最大值时点N的坐标．
