��Ŀ����
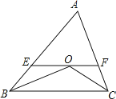
����Ŀ����Rt��ABC�У���BAC=90������O����ABC����ƽ����һ�㣬����OA���ӳ�OA����E��ʹ��AE=OA������OC������B��BD��OCƽ�У���ʹ��DBC=��OCB����BD=OC������DE.
(1)��ͼһ������O��Rt��ABC�ڲ�ʱ.

�ٰ����ⲹȫͼ�Σ�
�ڲ���DE��BC��������ϵ����֤��.
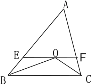
(2)��AB=AC(��ͼ��)���ҡ�OCB=30������OBC=15�������AED�Ĵ�С.


���𰸡�(1)�ٲ�ȫͼ�Σ���ͼһ�����������ڲ���DE=BC. ֤����������(2) ��AED=30����15��.
��������
��1���ٸ���Ҫ��ͼ�μ��ɽ�����⣮
�ڽ��ۣ�DE=BC������OD��BC��F������AF��֤��AFΪRt��ABCб�����ߣ�Ϊ��ODE����λ�ߣ����ɽ�����⣮
��2�����������Σ���ͼ���У�����O����ABC�ڲ�ʱ������OD��BC��F������AF���ӳ�CO��AF��M������BM��֤����BMA�ա�BMO��AAS�����Ƴ�AM=OM����BMO=��BMA=120�����Ƴ���AMO=120�������ɽ�����⣮��ͼ���У�����O����ABC�ⲿʱ������O����ABC�ڲ�ʱ������OD��BC��F������AF���ӳ�CO��AF��M������BM���ֱ���⼴�ɣ�
(1)�ٲ�ȫͼ�Σ���ͼһ��

�ڲ���DE=BC.
��ͼ������OD��BC�ڵ�F������AF

����BDF����COF��

���BDF����COF
��DF=OF��BF=CF
��F�ֱ�ΪBC��DO���е�
�ߡ�BAC=90����FΪBC���е㣬
��AF=![]() BC.
BC.
��OA=AE��FΪBC���е㣬
��AF=![]() ED.
ED.
��DE=BC
��2����ͼ���У�����O����ABC�ڲ�ʱ������OD��BC��F������AF���ӳ�CO��AF��M������BM��

�ɣ�1����֪��AFΪRt��ABCб�����ߣ�Ϊ��ODE����λ�ߣ�
��AB=AC��
��AF��ֱƽ���߶�BC��
��MB=MC���ߡ�OCB=30������OBC=15����
���MBC=��MCB=30����
�ߡ�BAC=90����AB=AC��
���ABC=��ACB=45������MBO=��MBA=15����
�ߡ�BAM=��BOM=45����BM=BM��
���BMA�ա�BMO��AAS����
��AM=OM����BMO=��BMA=120����
���AMO=120����
���MAO=��MOA=30����
���AED=��MAO=30����
��ͼ���У�����O����ABC�ⲿʱ������O����ABC�ڲ�ʱ������OD��BC��F������AF���ӳ�CO��AF��M������BM��

�ɡ�BOM=��BAM=45������֪A��B��M��O�ĵ㹲Բ��
���MAO=��MBO=30��-15��=15����
��DE��AM��
���AED=��MAO=15����
�������������������ġ�AED��ֵΪ15����30����