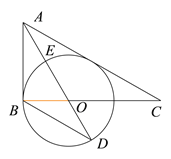МвДҝДЪИЭ
ЎҫМвДҝЎҝИзНјЈ¬ФЪЎчABCЦРЈ¬AB=ACЈ¬ЎПABCәНЎПACBөДЖҪ·ЦПЯҪ»УЪөгO.
(1) ҪбәПНјРОЈ¬ЗлДгРҙіцДгИПОӘХэИ·өДҪбВЫЈ»
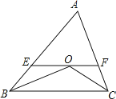
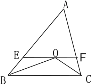
(2) №эOЧчEFЎОBCҪ»ABУЪEЈ¬Ҫ»ACУЪF. ЗлДгРҙіцНјЦРЛщУРөИСьИэҪЗРОЈ¬ІўМҪҫҝEFЎўBEЎўFCЦ®јдөД№ШПөЈ»

(3) ИфABЎЩACЈ¬ЖдЛыМхјюІ»ұдЈ¬НјЦР»№УРөИСьИэҪЗРОВрЈҝИфУРЈ¬ЗлРҙіцЛщУРөДөИСьИэҪЗРОЈ¬ИфГ»УРЈ¬ЗлЛөГчАнУЙЈ»ПЯ¶ОEFЎўBEЎўFCЦ®јдЈ¬ЙПГжМҪҫҝөДҪбВЫКЗ·с»№іЙБўЈҝ
Ўҫҙр°ёЎҝЈЁ1Ј©ҪбВЫЈәЎПABO=ЎПCBO=ЎПACO=ЎПBCOЈЁұҫМвҪбВЫІ»ОЁТ»Ј¬ХэИ·јҙҝЙЈ©Ј¬АнУЙПкјыҪвОцЈ»ЈЁ2Ј©өИСьИэҪЗРОУРЈәЎчABCЎўЎчAEFЈ¬ЎчBEOЈ¬ЎчCOFЈ¬ЎчBOCЈ»EFЎўBEЎўFCЦ®јдөД№ШПөEF=BE+CFЈ¬ АнУЙПкјыҪвОцЈ»ЈЁ3Ј©НјЦРөДөИСьИэҪЗРОУРЈәЎчBEOЈ¬ЎчCOF Ј»ҪбВЫИФИ»іЙБўЈ¬АнУЙПкјыҪвОц.
ЎҫҪвОцЎҝ
ЈЁ1Ј©Ј©ҪбВЫЈәЎПABO=ЎПCBO=ЎПACO=ЎПBCOЈ¬ёщҫЭөИСьИэҪЗРОөДРФЦКј°ҪЗЖҪ·ЦПЯөД¶ЁТејҙҝЙЦӨГчЈЁұҫМвҙр°ёІ»ОЁТ»Ј©Ј»ЈЁ2Ј©өИСьИэҪЗРОУРЈәЎчABCЎўЎчAEFЈ¬ЎчBEOЈ¬ЎчCOFЈ¬ЎчBOCЈ»EFЎўBEЎўFCЦ®јдөД№ШПөEF=BE+CFЈ¬УЙЈЁ1Ј©ҝЙөГЈ¬ЎчABCЎўЎчBOCКЗөИСьИэҪЗРОЈ»УЙЖҪРРПЯөДРФЦКј°өИСьИэҪЗРОөДРФЦКУлЕР¶ЁјҙҝЙЦӨөГЎчAEFКЗөИСьИэҪЗРОЈ»УЙЖҪРРПЯөДРФЦКј°ҪЗЖҪ·ЦПЯөД¶ЁТејҙҝЙЦӨөГЎчBEOЈ¬ЎчCOFКЗөИСьИэҪЗРОЈ¬EF=BE+CFЈ»ЈЁ2Ј©НјЦРөДөИСьИэҪЗРОУРЈәЎчBEOЈ¬ЎчCOF Ј»ҪбВЫИФИ»іЙБўЈ¬АаұИЈЁ2Ј©өД·Ҫ·ЁЦӨГчјҙҝЙ.
ЈЁ1Ј©ҪбВЫЈәЎПABO=ЎПCBO=ЎПACO=ЎПBCOЈ¬АнУЙИзПВЈә
ЎЯAB=ACЈ¬ЎаЎПABC=ЎПACBЈ®
ЎЯOBЖҪ·ЦЎПABCЈ¬OCЖҪ·ЦЎПACBЈ¬
ЎаЎПABO=ЎПCBO=ЎПACO=ЎПBCOЈ®
ЈЁ2Ј©өИСьИэҪЗРОУРЈәЎчABCЎўЎчAEFЈ¬ЎчBEOЈ¬ЎчCOFЈ¬ЎчBOCЈ»EFЎўBEЎўFCЦ®јдөД№ШПөEF=BE+CFЈ¬ АнУЙИзПВЈә
УЙЈЁ1Ј©ҝЙөГЈ¬ЎчABCЎўЎчBOCКЗөИСьИэҪЗРОЈ»
ЎЯEFЎОBCЈ¬
ЎаЎПABC=ЎПAEFЈ¬ЎПAFE=ЎПACB,
ЎЯЎПABC=ЎПACBЈ¬
ЎаЎПAEF=ЎПAFEЈ¬
ЎаAE=AF,
јҙЎчAEFКЗөИСьИэҪЗРОЈ»
ЎЯBOЖҪ·ЦЎПABCЈ¬
ЎаЎПEBO=ЎПOBCЈ»
ЎЯEFЎОBCЈ¬
ЎаЎПOBC=ЎПEOBЈ¬
ЎаЎПEBO=ЎПEOBЈ»
ЎаEO=BEЈ¬
ЎаЎчBEOКЗөИСьИэҪЗРОЈ»
Н¬АнҝЙөГOF=FCЈ¬
ЎаЎчCOFКЗөИСьИэҪЗРОЈ»
ЎаEO+OF=BE+FCЈ¬
јҙEF=BE+CFЈ®
ЈЁ3Ј©НјЦРөДөИСьИэҪЗРОУРЈәЎчBEOЈ¬ЎчCOF Ј»ҪбВЫИФИ»іЙБўЈ¬АнУЙИзПВЈә
ЎЯBOЖҪ·ЦЎПABCЈ¬
ЎаЎПEBO=ЎПOBCЈ»
ЎЯEFЎОBCЈ¬
ЎаЎПOBC=ЎПEOBЈ¬
ЎаЎПEBO=ЎПEOBЈ»
ЎаEO=BEЈ¬
ЎаЎчBEOКЗөИСьИэҪЗРОЈ»
Н¬АнҝЙөГOF=FCЈ¬
ЎаЎчCOFКЗөИСьИэҪЗРОЈ»
ЎаEO+OF=BE+FCЈ¬
јҙEF=BE+CFЈ®

ЎҫМвДҝЎҝУР20ҝрйЩЧУЈ¬ТФГҝҝр20З§ҝЛОӘұкЧјЈ¬і¬№э»тІ»ЧгөДІҝ·Ц·ЦұрУГХэКэ»тёәКэАҙұнКҫЈ¬јЗВјИзПВЈә
УлұкЧјЦШБҝөДІо(өҘО»ЈәЗ§ҝЛ) | Јӯ2 | Јӯ1.5 | Јӯ1 | 0 | 1 | 1.5 |
ҝр Кэ | 1 | 4 | 2 | 3 | 2 | 8 |
(1)ЗуЧоЦШөДТ»ҝрұИЧоЗбөДТ»ҝрЦШ¶аЙЩЈҝ
(2)Зу20ҝрйЩЧУөДЧЬЦШБҝКЗ¶аЙЩЗ§ҝЛЈҝ