ΧβΡΩΡΎ»ί
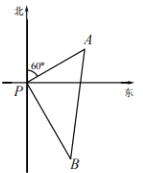
ΓΨΧβΡΩΓΩ»γΆΦΘ®1Θ©Θ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§ΒψAΘ§BΒΡΉχ±ξΖ÷±πΈΣΘ®©¹1Θ§0Θ©Θ§Θ®3Θ§0Θ©Θ§ΫΪœΏΕΈABœ»œρ…œΤΫ“Τ2ΗωΒΞΈΜ≥ΛΕ»Θ§‘Όœρ”“ΤΫ“Τ1ΗωΒΞΈΜ≥ΛΕ»Θ§ΒΟΒΫœΏΕΈCDΘ§Ν§Ϋ”ACΘ§BDΘ§ΙΙ≥…ΤΫ––ΥΡ±Ώ–ΈABDCΘ°
Θ®1Θ©«κ–¥≥ωΒψCΒΡΉχ±ξΈΣΓΓ ΓΓΘ§ΒψDΒΡΉχ±ξΈΣΓΓ ΓΓΘ§SΥΡ±Ώ–ΈABDCΓΓ ΓΓΘΜ
Θ®2Θ©ΒψQ‘Ύy÷α…œΘ§«“SΓςQABΘΫSΥΡ±Ώ–ΈABDCΘ§«σ≥ωΒψQΒΡΉχ±ξΘΜ
Θ®3Θ©»γΆΦΘ®2Θ©Θ§ΒψP «œΏΕΈBD…œ»Έ“β“ΜΗωΒψΘ®≤Μ”κBΓΔD÷ΊΚœΘ©Θ§Ν§Ϋ”PCΓΔPOΘ§ ‘ΧΫΥςΓœDCPΓΔΓœCPOΓΔΓœBOP÷°ΦδΒΡΙΊœΒΘ§≤Δ÷ΛΟςΡψΒΡΫα¬έΘ°

ΓΨ¥πΑΗΓΩΘ®1Θ©Θ®0Θ§2Θ©Θ§Θ®4Θ§2Θ©Θ§8ΘΜΘ®2Θ©Q(0Θ§4)ΜρQ(0Θ§©¹4)ΘΜΘ®3Θ©ΓœCPOΘΫΓœDCP+ΓœBOPΘ§÷ΛΟςΦϊΫβΈω
ΓΨΫβΈωΓΩ
Θ®1Θ©ΗυΨίΤΫ“Τ÷±Ϋ”ΒΟΒΫΒψCΘ§DΉχ±ξΘ§”ΟΟφΜΐΙΪ ΫΦΤΥψSΥΡ±Ώ–ΈABDCΦ¥Ω…ΘΜ
Θ®2Θ©…η≥ωQΒΡΉχ±ξΘ§OQΘΫ|m|Θ§”ΟSΓςQABΘΫSΥΡ±Ώ–ΈABDCΫ®ΝΔΖΫ≥ΧΘ§ΫβΖΫ≥ΧΦ¥Ω…ΘΜ
Θ®3Θ©ΉςPEΓΈABΫΜ y ÷α ”Ύ Βψ EΘ§άϊ”ΟΝΫ÷±œΏΤΫ––Θ§ΡΎ¥μΫ«œύΒ»Φ¥Ω…ΒΟ≥ωΫα¬έΘ°
ΫβΘΚΘ®1Θ©ΓΏœΏΕΈABœ»œρ…œΤΫ“Τ2ΗωΒΞΈΜ≥ΛΕ»Θ§‘Όœρ”“ΤΫ“Τ1ΗωΒΞΈΜ≥ΛΕ»Θ§ΒΟΒΫœΏΕΈCDΘ§
«“AΘ®©¹1Θ§0Θ©Θ§BΘ®3Θ§0Θ©Θ§
ΓύCΘ®0Θ§2Θ©Θ§DΘ®4Θ§2Θ©ΘΜ
ΓΏABΘΫ4Θ§OCΘΫ2Θ§
ΓύSΥΡ±Ώ–ΈABDCΘΫABΓΝOCΘΫ4ΓΝ2=8ΘΜ
Ι ¥πΑΗΈΣΘΚΘ®0Θ§2Θ©ΘΜΘ®4Θ§2Θ©ΘΜ8ΘΜ
Θ®2Θ©ΓΏΒψQ‘Ύy÷α…œΘ§…ηQΘ®0Θ§mΘ©Θ§
ΓύOQΘΫ|m|Θ§
ΓύSΓςQABΘΫ![]() ΓΝABΓΝOQΘΫ
ΓΝABΓΝOQΘΫ![]() ΓΝ4ΓΝ|m|ΘΫ2|m|Θ§
ΓΝ4ΓΝ|m|ΘΫ2|m|Θ§
ΓΏSΥΡ±Ώ–ΈABDCΘΫ8Θ§
Γύ2|m|ΘΫ8Θ§
ΓύmΘΫ4ΜρmΘΫ©¹4Θ§
ΓύQΘ®0Θ§4Θ©ΜρQΘ®0Θ§©¹4Θ©Θ°
Θ®3Θ©»γΆΦΘ§
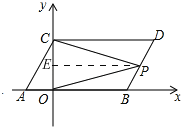
ΓΏœΏΕΈCD «œΏΕΈABΤΫ“ΤΒΟΒΫΘ§
ΓύCDΓΈABΘ§
ΉςPEΓΈABΫΜ y ÷α ”Ύ Βψ EΘ§
ΓύCDΓΈPEΘ§
ΓύΓœCPEΘΫΓœDCPΘ§
ÿPEøABȧ
ΓύΓœOPEΘΫΓœBOPΘ§
ΓύΓœCPOΘΫΓœCPE+ΓœOPEΘΫΓœDCP+ΓœBOPΘ§
ΓύΓœCPOΘΫΓœDCP+ΓœBOPΘ°