题目内容
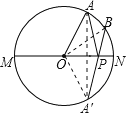
【题目】如图所示，点A是半圆上的一个三等分点，B是劣弧
的中点，点P是直径MN上的一个动点，⊙O的半径为1，则AP+PB的最小值_______．
【答案】
【解析】试题分析：首先找出点A关于MN对称的对称点A'，AP+BP的最小值就是A′B的长度．
试题解析：如图，作点A关于MN的对称点A′，连接BA′交圆于P，则点P即是所求作的点，
∵A是半圆上一个三等分点，
∴∠AON=∠A′ON=360°÷2÷3=60°，
又∵点B是弧AN的中点，
∴∠BON=
∠AON=×60°="30°"
∴∠A′OB=∠A′ON+∠BON=60°+30°=90°
在Rt△A′OB中，由勾股定理得：A′B2=A′O2+BO2="1+1=2"
得：A′B=，
所以：AP+BP的最小值是.
练习册系列答案
相关题目
