题目内容
【题目】如图,在平面直角坐标系中,每个小正方形边长为1,点A的坐标为(-2,3)、点B的坐标为(-3,1)、点C的坐标为(1,-2)
(1)作出△ABC关于y轴对称的△A′B′C′(其中A′、B′、C′分别是A、B、C的对应点,不写画法).
(2) 直接写出A′、B′、C三点的坐标.
(3)在x轴上求作一点P,使PA+PB的值最小.(简要写出作图步骤)

【答案】(1)作图见解析;(2)A′(2,3)、B′(3,1)、C′(-1,2);(3)作图见解析.
【解析】试题分析:(1)(1)首先确定A、B、C三点关于y轴对称点位置,再连接即可;
(2)由平面直角坐标系即可确定三点坐标;
(3)作点B关于x轴对称点B",连接AB"与x轴的交点即为所求的点P.
试题解析:(1),如图所示△A′B′C′;
(2) A′(2,3)、B′(3,1)、C′(-1,2);
(3)如图所示P点即为所求.
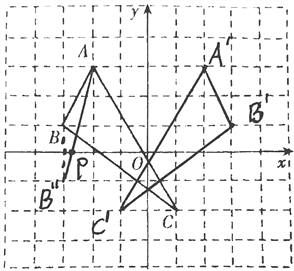
找到点B关于x轴的对称点B′′,连接AB′′交x轴于点P,此时PA+PB的值最小.

练习册系列答案
相关题目