Question

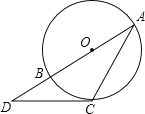
【题目】如图,O的直径AB=2,点D在AB的延长线上,DC与O相切于点C,连接AC.若∠A=30°,则CD长为( )

A. B. C. D.

Answer 1

【答案】D

【解析】

先连接BC，OC，由于AB 是直径，可知∠BCA=90°，而∠A=30°，易求∠CBA，又DC是切线，利用弦切角定理可知∠DCB=∠A=30°，再利用三角形外角性质可求∠D，再由切线的性质可得∠BCD=∠A=30°，∠OCD=90°，易得OD，由勾股定理可得CD．

如图所示，连接BC，OC，

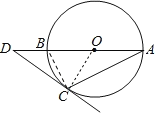
∵AB是直径,

∴∠BCA=90°，

又∵∠A=30°，

∴∠CBA=90°30°=60°，

∵DC是切线，

∴∠BCD=∠A=30°,∠OCD=90°，

∴∠D=∠CBA∠BCD=60°30°=30°，

∵AB=2，

∴OC=1，

∴OD=2，

∴CD=，

故选D.