题目内容
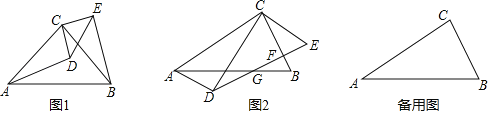
【题目】(1)△ABC和△CDE是两个等腰直角三角形,如图1,其中∠ACB=∠DCE=90°,连结AD、BE,求证:△ACD≌△BCE.
(2)△ABC和△CDE是两个含30°的直角三角形,其中∠ACB=∠DCE=90°,∠CAB=∠CDE=30°,CD<AC,△CDE从边CD与AC重合开始绕点C逆时针旋转一定角度α(0°<α<180°);
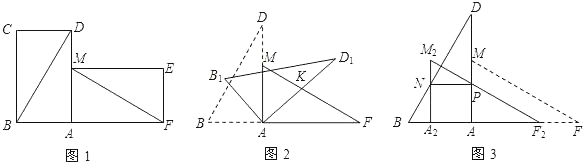
①如图2,DE与BC交于点F,与AB交于点G,连结AD,若四边形ADEC为平行四边形,求![]() 的值;
的值;
②若AB=10,DE=8,连结BD、BE,当以点B、D、E为顶点的三角形是直角三角形时,求BE的长.
【答案】(1)见解析;(2)①![]() ;②BE的长为﹣2
;②BE的长为﹣2![]() +
+![]() 或
或![]() .
.
【解析】
(1)由等腰直角三角形的性质得出AC=BC,CD=CE,∠ACB=∠DCE,证出∠ACD=∠BCE,由SAS得出△ACD≌△BCE即可;
(2)①连接CG,由平行四边形的性质得出∠ADE+∠CED=180°,证出∠ADC=∠ADE﹣∠CDE=90°,A、D、G、C四点共圆,由圆周角定理得出∠AGC=∠ADC=90°,由直角三角形的性质得出CG=![]() AC,AG=
AC,AG=![]() CG,CG=
CG,CG=![]() BG,即可得出结果;
BG,即可得出结果;
②分三种情况:
当∠BED=90°时,证明△ACD∽△BCE,得出![]() =
=![]() ,得出AD=
,得出AD=![]() BE,证出A、D、E共线,在Rt△ABE中,由勾股定理得出方程,解方程即可;
BE,证出A、D、E共线,在Rt△ABE中,由勾股定理得出方程,解方程即可;
当∠DBE=90°时,作CF⊥AB于F,由勾股定理得出DF=![]() ,得出AD=
,得出AD=![]() ,即可得出BE的长;
,即可得出BE的长;
当∠BDE=90°时,作BG⊥CD于G,设DG=x,则CG=4![]() ﹣x,BG=
﹣x,BG=![]() x,在Rt△BCG中,由勾股定理得出方程,解方程即可.
x,在Rt△BCG中,由勾股定理得出方程,解方程即可.
(1)证明:∵△ABC和△CDE是两个等腰直角三角形,
∴AC=BC,CD=CE,∠ACB=∠DCE,
∴∠ACD=∠BCE,
在△ACD和△BCE中,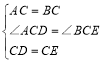 ,
,
∴△ACD≌△BCE(SAS);
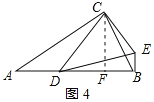
(2)解:①连接CG,如图2所示:
∵四边形ADEC为平行四边形,
∴AD∥CE,
∴∠ADE+∠CED=180°,
∵∠CED=90°﹣∠CDE=90°﹣30°=60°,
∴∠ADE=120°,
∴∠ADC=∠ADE﹣∠CDE=90°,
∵∠CAB=∠CDE=30°,
∴A、D、G、C四点共圆,
∴∠AGC=∠ADC=90°,
∵∠CAB=30°,
∴CG=![]() AC,AG=
AC,AG=![]() CG,∠BCG=30°,
CG,∠BCG=30°,
∴CG=![]() BG,即BG=
BG,即BG=![]() CG,
CG,
∴![]() =3;
=3;
②分三种情况:
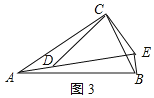
当∠BED=90°时,如图3所示:
∵△ABC和△CDE是两个含30°的直角三角形,∠ACB=∠DCE=90°,∠CAB=∠CDE=30°,
∴∠ACD=∠BCE,![]() ,
,
∴△ACD∽△BCE,
∴![]() =
=![]() ,
,
∴AD=![]() BE,
BE,
∴∠ADC=∠BEC=90°+∠CED=90°+60°=150°,
∵∠CDE=30°,
∴∠CDE+∠ADC=180°,
∴A、D、E共线,
在Rt△ABE中,由勾股定理得:AE2+BE2=AB2,
即(![]() BE+8)2+BE2=102,
BE+8)2+BE2=102,
解得:BE=﹣2![]() ±
±![]() (负值舍去),
(负值舍去),
∴BE=﹣2![]() +
+![]() ;
;
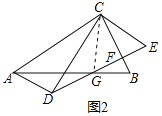
当∠DBE=90°时,如图4所示:
作CF⊥AB于F,则∠BCF=30°,
∴BF=![]() BC,
BC,
∵∠ACB=∠DCE=90°,∠CAB=∠CDE=30°,
∴BC=![]() AB=5,CE
AB=5,CE![]() DE=4,
DE=4,
∴CD=![]() CE=4
CE=4![]() ,
,
∴BF=![]() BC=
BC=![]() ,
,
∴CF=![]() BF=
BF=![]()
![]() ,
,
∴DF=![]() ,
,
∵AB=AD+DF+BF,
∴AD=10﹣![]() ,
,
∴BE=![]() ;
;
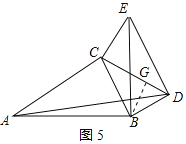
当∠BDE=90°时,如图5所示:
作BG⊥CD于G,
则∠BDG=∠BDE﹣∠CDE=60°,
∴∠DBG=30°,
∴BD=2DG,BG=![]() DG,
DG,
设DG=x,则CG=4![]() ﹣x,BG=
﹣x,BG=![]() x,
x,
在Rt△BCG中,由勾股定理得:CG2+BG2=BC2,
即(4![]() ﹣x)2+(
﹣x)2+(![]() x)2=52,
x)2=52,
整理得:4x![]() x+23=0,
x+23=0,
∵△=(﹣8![]() )2﹣4×4×23<0,
)2﹣4×4×23<0,
∴此方程无解;
综上所述,当以点B、D、E为顶点的三角形是直角三角形时,BE的长为﹣2![]() +
+![]() 或
或![]() .
.