题目内容

【题目】如图，在△ABC中，∠A＝90°，AC＝AB，CD平分∠ACB，DE⊥BC于点E，若BC＝15 cm，则△DEB的周长为（ ）

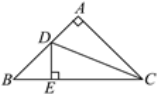
A.14 cmB.15 cm

C.16 cmD.17 cm

【答案】B

【解析】

先根据ASA判定△ACD≌△ECD得出AC=EC，AD=ED，再将其代入△DEB的周长中，通过边长之间的转换得到，周长=BD+DE+EB=BD+AD+EB=AB+BE

=AC+EB=CE+EB=BC，所以为15cm．

解：∵CD平分∠ACB，DE⊥BC于E，∠A=90°，
∵AD=ED，

∵CD= CD，
∴△ACD≌△ECD，
∴AC=EC，

∵AC＝AB，

∴AB=EC，

∴△DEB的周长为：DE+BE+BD=AD+BD+BE=AB+BE=AC+BE=EC+BE=BC=15cm．

故选：B.

练习册系列答案
相关题目

【题目】如图，中，∠BAC=90°，AB=AC，F是BC上一点，BDAF的延长线与D，CEAF于E，已知CE=5，BD=2，ED=__________

【题目】如图1，过等边三角形ABC边AB上一点D作DE∥BC交边AC于点E，分别取BC，DE的中点M，N，连接MN．

（1）发现：在图1中，，说明理由；

（2）探索：如图2，将△ADE绕点A旋转，请求出的值；

（3）拓展：如图3，△ABC和△ADE是等腰三角形，且∠BAC=∠DAE，M，N分别是底边BC，DF的中点，若BD⊥CE，请直接写出的值．

【题目】如图，在△ABC中，AB＝AC，∠BAC＝30°，点D是△ABC内一点，DB＝DC，∠DCB＝30°，点E是BD延长线上一点，AE＝AB．

（1）求证：△ABD≌△ACD．

（2）求∠ADE的度数．

（3）试猜想线段DE，AD，DC之间的数量关系，并证明你的结论．

【题目】已知抛物线与轴交于，两点，交轴于点．

求抛物线的解析式；

点是第二象限内一点，过点作轴交抛物线于点，过点作轴于点，连接、，若．求的值并直接写出的取值范围（利用图完成你的探究）．

如图，点是线段上一动点（不包括点、），轴交抛物线于点，，交直线于点，设点的横坐标为，求的周长．

【题目】如图1，在Rt△ABC中，∠ACB=90°，AC=6cm，BC=8cm，点P从A出发沿AC向C点以1厘米/秒的速度匀速移动；点Q从C出发沿CB向B点以2厘米/秒的速度匀速移动．点P、Q分别从起点同时出发，移动到某一位置时所需时间为t秒．

（1）当t=2时，求线段PQ的长度；

（2）当t为何值时，△PCQ的面积等于5cm2？

（3）在P、Q运动过程中，在某一时刻，若将△PQC翻折，得到△EPQ，如图2，PE与AB能否垂直？若能，求出相应的t值；若不能，请说明理由．

【题目】如图，C为线段AE上一动点（不与点A、E重合），在AE同侧分别作正△ABC和正△CDE，AD与BE交于点O，AD与BC交于点P，BE与CD交于点Q，连接PQ．以下五个结论：①AD=BE；②PQ∥AE；③AP=BQ；④DE=DP；⑤∠AOB=60°．

恒成立的结论有 ．（把你认为正确的序号都填上）

【题目】已知关于x的一元二次方程(a＋c)x2＋2bx＋(a－c)＝0，其中a，b，c分别为△ABC三边的长．

(1)如果x＝－1是方程的根，试判断△ABC的形状，并说明理由；

(2)如果方程有两个相等的实数根，试判断△ABC的形状，并说明理由．

【题目】某商场老板对一种新上市商品的销售情况进行记录，已知这种商品进价为每件40元，经过记录分析发现，当销售单价在40元至90元之间（含40元和90元）时，每月的销售量y（件）与销售单价x（元）之间的关系可近似地看作一次函数，其图象如图所示．

（1）求y与x的函数关系式．

（2）设商场老板每月获得的利润为P（元），求P与x之间的函数关系式；

（3）如果想要每月获得2400元的利润，那么销售单价应定为多少元？

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网