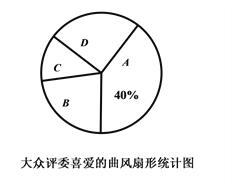
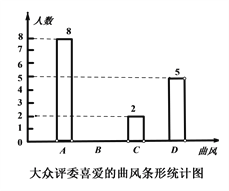
题目内容
【题目】将正整数1至2018按一定的规律排成下图所示的10列,规定从上到下依次为1行、2行、3行…,从左到右依次为第1列至第10列.

(1)数2018在 行, 列;
(2)把图中带阴影的3个方相当作一个整体平移,设被框住的3个数中,最大的一个数为x.
①求被框住的三个数的和(用含x的式子表示);
②被框住的三个数的和能否于2017?若能,求出x的值;若不能,请说明理由.
【答案】(1)202,8;(2)①3x﹣20,②能,被框住的三个数的和能等于2017.x=679.
【解析】
(1)用2018除以10即可得出答案;
(2)①先根据图表将另外两个数用x表示出来,再求和即可;
②令①的式子等于2017,根据所求出的整数x的值即可得出答案.
(1)![]()
则按题中图表可知,2018在第202行第8列
故答案为:202,8;
(2)①根据图表可得,其他两个数为![]()
则三个数的和为![]() ;
;
②令![]()
解方程,得![]()
又因![]()
则数字679在第68行第9列,符合题意
答:被框住的三个数的和能等于2017,此时x的值为679.

练习册系列答案
相关题目