题目内容
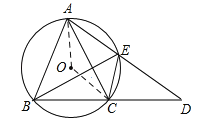
【题目】如图,△ABC内接于⊙O,且AB=AC.延长BC到点D,使CD=CA,连接AD交⊙O于点E.
(1)求证:△ABE≌△CDE;
(2)填空:
①当∠ABC的度数为 时,四边形AOCE是菱形;
②若AE=6,BE=8,则EF的长为 .

【答案】(1)证明见解析(2)①60②![]()
【解析】分析:(1)根据AAS证明两三角形全等;
(2)①先证明∠AOC=∠AEC=120°,∠OAE=∠OCE=60°,可得AOCE,由OA=OC可得结论;
②根据(1)中的全等得:BE=DE=8,AE=CE=6,证明△ECD∽△CFB,列式可得:![]() =
=![]() ,证明△AEF∽△BCF,则可得EF的长.
,证明△AEF∽△BCF,则可得EF的长.
详解:(1)证明:∵AB=AC,CD=CA,∴∠ABC=∠ACB,AB=CD.
∵四边形ABCE是圆内接四边形,∴∠ECD=∠BAE,∠CED=∠ABC.
∵∠ABC=∠ACB=∠AEB,∴∠CED=∠AEB,∴△ABE≌△CDE(AAS);
(2)①当∠ABC的度数为60°时,四边形AOCE是菱形;
理由是:连接AO、OC.
∵四边形ABCE是圆内接四边形,∴∠ABC+∠AEC=180°.
∵∠ABC=60,∴∠AEC=120°=∠AOC.
∵OA=OC,∴∠OAC=∠OCA=30°.
∵AB=AC,∴△ABC是等边三角形,∴∠ACB=60°.
∵∠ACB=∠CAD+∠D.
∵AC=CD,∴∠CAD=∠D=30°,∴∠ACE=180°﹣120°﹣30°=30°,∴∠OAE=∠OCE=60°,∴四边形AOCE是平行四边形.
∵OA=OC,∴AOCE是菱形;
②由(1)得:△ABE≌△CDE,∴BE=DE=8,AE=CE=6,∴∠D=∠EBC.
∵∠CED=∠ABC=∠ACB,∴△ECD∽△CFB,∴![]() =
=![]() .
.
∵∠AFE=∠BFC,∠AEB=∠FCB,∴△AEF∽△BCF,∴![]() =
=![]() ,∴EF=
,∴EF=![]() =
=![]() .
.
故答案为:①60°;②![]() .
.