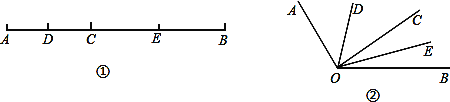
题目内容
【题目】阅读下面材料并回答问题：
点A，B在数轴上分别表示数a，b，A，B两点之间的距离表示为AB．
当A，B两点中有一点在原点时：
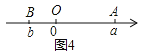
不妨设A在原点，如图1，AB=OB=|b|=|a-b|；
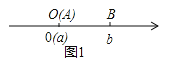
当A，B两点都不在原点时：
①如图2，点A，B都在原点的右边，AB=OB-OA=|b|-|a|=b-a=|a-b|；
②如图3，点A，B都在原点左边，AB=OB-OA=|b|-|a|=（-b）-（-a）=|a-b|；
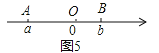
③如图4，点A，B在原点的两边，AB=OA+OB=|a|+|b|=a+（-b）=|a-b|；
综上，数轴上A，B两点之间的距离AB=|a-b|．
（1）回答问题：数轴上表示2和5的两点之间的距离是 ，数轴上表示-2和-5的两点之间的距离是 ，数轴上表示1和-3的两点之间的距离是 ，数轴上表示x和-1的两点之间的距离是 .
（2）如图5，若|a-b|=2013，且OA=2OB，求a+b的值．
（3）结合两点之间的距离，若点M表示的数为x，当代数式|x+1|+|x-2|取最小值时，相应x的取值范围是
【答案】（1）3，3，4，|x+1|；（2）-671；（3）-1≤x≤2．
【解析】试题分析：（1）根据两点间的距离公式即可求解；
（2）根据题意列出关于
的方程，求出方程的解即可得到
的值；
（3）当
大于等于0，且
小于等于0时，原式取得最小值，求出这个最小值即可．
试题解析：(1)数轴上表示2和5的两点之间的距离是52=3,数轴上表示2和5的两点之间的距离是2(5)=3,数轴上表示1和3的两点之间的距离是1(3)=4，数轴上表示x和1的两点之间的距离是|x+1|.
(2)∵|ab|=2013，且OA=2OB，
∴3b=2013，解得b=671，
a=2b=1342，
a+b=1342+671=671.
故a+b的值是671.
(3)数形结合，若|x+1|+|x2|取最小值，那么表示x的点M在1和2之间的线段上，
所以
故答案为：3，3，4，|x+1|； 
