题目内容
如图,平面直角坐标系中,O为坐标原点,等腰梯形ABCD四个顶点都在抛物线y=ax2+bx+c上,其中点A、B在x轴上,点D在 轴上,且CD∥AB, 已知S梯形ABCD=8,tan∠DAO=4,点B的坐标为(2,0),点E坐标为(0,-1).
轴上,且CD∥AB, 已知S梯形ABCD=8,tan∠DAO=4,点B的坐标为(2,0),点E坐标为(0,-1).
(1)求此抛物线的解析式;
(2)若△OEB从点B开始以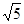 个单位每秒的速度沿BD向终点D匀速运动. 设运动时间为t秒,在整个运动过程中,当边OE与线段AD相交时,求运动时间t的取值范围;
个单位每秒的速度沿BD向终点D匀速运动. 设运动时间为t秒,在整个运动过程中,当边OE与线段AD相交时,求运动时间t的取值范围;
(3)能否将△OEB绕平面内某点旋转90°后使得△OEB的两个顶点落在x轴上方的抛物线上,若能,请直接写出旋转中心的坐标,若不能,请说明理由.
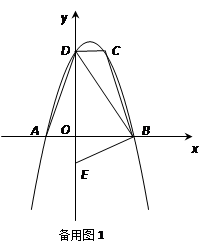

解:(1)在等腰梯形ABCD中,S梯形ABCD=8
∴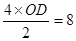
∴OD=4 ∴D(0,4)
∵tan∠DAO=4 ∴OA="1"
∴A(-1,0)
把A(-1,0)、B(2,0)、D(0,4)代入y=ax2+bx+c得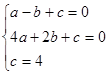 ∴
∴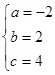
∴y=-2x2+2x+4
(2)当点O在线段AD上时,如图,
BB1=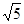 t B1O1=2 B1H="2" t BH= t
t B1O1=2 B1H="2" t BH= t
B1G=2-t O1G=2-(2-t)= t
由△DO1G∽△DAO得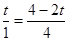 ∴
∴
当点E在线段AD上时,如图,
BB1=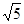 t B1H="2" t BH= t
t B1H="2" t BH= t
∵B1O1=2
∴E1G=t DG=4-(2 t-1)=5-2 t
由△DE1G∽△DAO得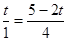 ∴
∴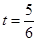
∴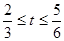
(3)(-2,2) (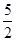 ,
, ) (3,
) (3, ) (-1,
) (-1, )
)
解析

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
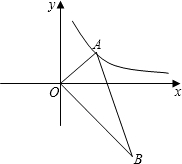 如图,平面直角坐标系中,O为直角三角形ABC的直角顶点,∠B=30°,锐角顶点A在双曲线
如图,平面直角坐标系中,O为直角三角形ABC的直角顶点,∠B=30°,锐角顶点A在双曲线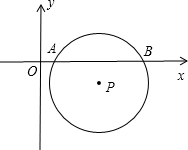 =2
=2 如图,平面直角坐标系中,OB在x轴上,∠ABO=90°,点A的坐标为(1,2).将△AOB绕点A逆时针旋转90°,则点O的对应点C的坐标为( )
如图,平面直角坐标系中,OB在x轴上,∠ABO=90°,点A的坐标为(1,2).将△AOB绕点A逆时针旋转90°,则点O的对应点C的坐标为( )
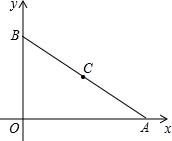 如图在平面直角坐标系中,A点坐标为(8,0),B点坐标为(0,6)C是线段AB的中点.请问在y轴上是否存在一点P,使得以P、B、C为顶点的三角形与△AOB相似?若存在,求出P点坐标;若不存在,说明理由.
如图在平面直角坐标系中,A点坐标为(8,0),B点坐标为(0,6)C是线段AB的中点.请问在y轴上是否存在一点P,使得以P、B、C为顶点的三角形与△AOB相似?若存在,求出P点坐标;若不存在,说明理由.