题目内容
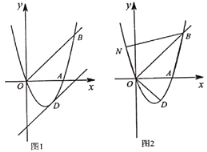
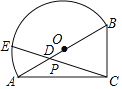
【题目】如图，一块∠BAC为30°的直角三角板ABC的斜边AB与量角器的直径恰好重合，点E在量角器的圆弧边缘处从A到B运动，连接CE，交直径AB于点D．
(1)当点E在量角器上对应的刻度是90°时，则∠ADE的度数为______；
(2)若AB=8，P为CE的中点，当点E从A到B的运动过程中，点P也随着运动，则点P所走过的路线长为______．
【答案】75° 2π
【解析】
(1)连接OE．根据∠ACE=
∠AOE=45°，∠ADE=∠A+∠ACE求解即可；
(2)连接OP，设OC的中点为O′．由PE=PC，推出OP⊥EC，推出∠OPC=90°，推出点P的运动轨迹是以OC为直径的半圆，由此即可解决问题；
解：(1)如图，连接OE．
∵直角三角板ABC的斜边AB与量角器的直径恰好重合，
∴点A，E，B，C共圆，
∵点E对应的刻度是90°，
∴∠AOE=90°，
∴∠ACE=∠AOE=45°，
∴∠ADE=∠A+∠ACE=75°．
故答案为75°．
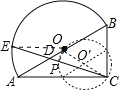
(2)连接OP，设OC的中点为O′．
∵PE=PC，
∴OP⊥EC，
∴∠OPC=90°，
∴点P的运动轨迹是以OC为直径的半圆，
∵OC=AB=4，
∴OO′=OC=2，
∴点P的运动路径的长为π2=2π，
故答案为2π
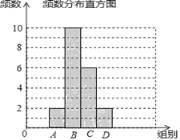
【题目】张老师把微信运动里“好友计步榜”排名前20的好友一天行走的步数做了整理，绘制了如下不完整的统计图表：
组别 | 步数分组 | 频率 |
A | x＜6000 | 0.1 |
B | 6000≤x＜7000 | 0.5 |
C | 7000≤x＜8000 | m |
D | x≥8000 | n |
合计 | 1 |
根据信息解答下列问题：
（1）填空：m＝ ，n＝ ；并补全条形统计图；
（2）这20名朋友一天行走步数的中位数落在 组；（填组别）
（3）张老师准备随机给排名前4名的甲、乙、丙、丁中的两位点赞，请求出甲、乙被同时点赞的概率．
