Question

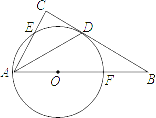
【题目】如图，抛物线交轴于点、，(左右)，交y轴于点C，△AOC的周长为12，sin∠CBA=，则下列结论：①A点坐标（-3，0）；②a=；③点B坐标(8，0)；④对称轴x=.其中正确的有( )个.

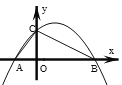
A. 4B. 3C. 2D. 1

Answer 1

【答案】A

【解析】

令=0，解得x=-3，x=k，即可得A点坐标为（-3，0）；由△AOC的周长为12可得AC+OC=9,再由即可求得AC=5,OC=4；在Rt△BOC中利用三角函数求得BC=4.在Rt△BOC中，由勾股定理求得OB=8，即可得点B坐标为(8，0)；所以抛物线的解析式为，抛物线的对称轴为；由OC=4,可得点C坐标为(0，4)；把C (0，4)代入求得a=.

令=0，解得x=-3，x=k，

∴A点坐标为（-3，0）；

∴OA=3；

∵△AOC的周长为12，

∴AC+OC=9,

∵,

∴AC=5,OC=4,

在Rt△BOC中，sin∠CBA=，

∴sin∠CBA=,

∴BC=4.

在Rt△BOC中，由勾股定理求得OB=8，

∴点B坐标为(8，0)；

∴抛物线的解析式为，

抛物线的对称轴为；

∵OC=4,

∴点C坐标为(0，4)；

把C (0，4)代入求得a=.

综上，正确的结论为①②③④，共4个.

故选A.