题目内容
【题目】设双曲线![]() 与直线
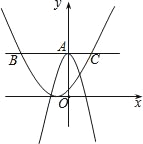
与直线![]() 交于A,B两点(点A在第三象限),将双曲线在第一象限的一支沿射线BA的方向平移,使其经过点A,将双曲线在第三象限的一支沿射线AB的方向平移,使其经过点B,平移后的两条曲线相交于P,Q两点,此时我们称平移后的两条曲线所围部分(如图中阴影部分)为双曲线的“眸”,PQ为双曲线的“眸径”,当双曲线
交于A,B两点(点A在第三象限),将双曲线在第一象限的一支沿射线BA的方向平移,使其经过点A,将双曲线在第三象限的一支沿射线AB的方向平移,使其经过点B,平移后的两条曲线相交于P,Q两点,此时我们称平移后的两条曲线所围部分(如图中阴影部分)为双曲线的“眸”,PQ为双曲线的“眸径”,当双曲线![]() 的眸径为9时,
的眸径为9时,![]() 的值为_____.
的值为_____.

【答案】![]()
【解析】
以 PQ 为边,作矩形 PQQ’P’交双曲线于点 P’、 Q′,联立直线AB及双曲线解析式成方程组,通过解方程组可求出点 A 、 B 的坐标,由 PQ 的长度可得出点 P 的坐标(点 P 在直线 y = - x 上找出点 P的坐标),由图形的对称性结合点 A 、B 和 P 的坐标可得出点 P’ 的坐标,再利用反比例函数图象上点的坐标特征即可得出关于 k 的一元一次方程,解之即可得出结论.
解:以 PQ 为边,作矩形 PQQ’P’交双曲线于点 P 、Q′,如图所示.

联立直线 AB 及双曲线解析式成方程组
解得
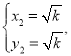
则有点A的坐标为![]() 点B的坐标为
点B的坐标为![]()
又PQ为9,求得点P坐标为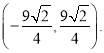
根据图形的对称性可知![]() 得到P’坐标为
得到P’坐标为
将其代入双曲线![]() ,
,
有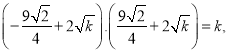
解得![]()
故答案为![]()

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目