题目内容
【题目】在平面直角坐标系
中，抛物线
（
）与
轴交于
、
两点（点在点左侧），与
轴交于点
，该抛物线的顶点
的纵坐标是
.
（1）求点、的坐标；
（2）设直线与直线
关于该抛物线的对称轴对称，求直线的表达式；
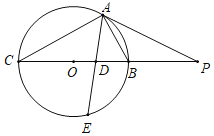
（3）平行于轴的直线
与抛物线交于点
、
,与直线交于点
.若
，结合函数图象，求
的取值范围.
【答案】（1）A(-3，0)，B(1 ，0)；（2）
；（3）
.
【解析】
（1）根据顶点坐标公式列式求出m的值，得到函数解析式，再求A、B即可；
（2）求出点C、A关于
的对称点坐标E、B，用待定系数法求直线的表达式即可；
（3）由抛物线对称性可得
，然后根据
的取值范围即可得到结果.
解：（1）∵抛物线
（
）的顶点
的纵坐标是
∴
，解得
∴
令
，则
，
∴A(-3，0) B(1 ，0)
（2）由题意，抛物线的对称轴为
点C（0 ，-3）的对称点坐标是E（-2 ，-3）
点A(-3 ，0)的对称点坐标是B(1 ，0)
设直线的表达式为
∵ 点E（-2 ，-3）和点B(1 ，0)在直线上
∴
解得
∴直线的表达式为
（3）由对称性可知 
，得
∵
∴
金牌教辅培优优选卷期末冲刺100分系列答案
【题目】丁老师为了解所任教的两个班的学生数学学习情况，对数学进行了一次测试，获得了两个班的成绩（百分制），并对数据（成绩）进行整理、描述和分析，下面给出了部分信息．
①A、B两班学生（两个班的人数相同）数学成绩不完整的频数分布直方图如下（数据分成5组：x<60，60≤x<70，70≤x<80，80≤x<90，90≤x≤100）：
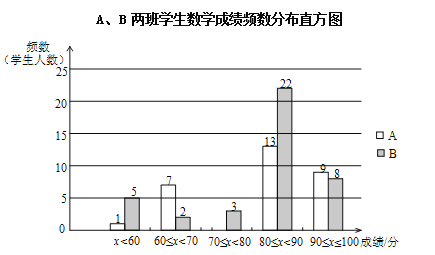
②A、B两班学生测试成绩在80≤x<90这一组的数据如下：
A班：80 80 82 83 85 85 86 87 87 87 88 89 89
B班：80 80 81 81 82 82 83 84 84 85 85 86 86 86 87 87 87 87 87 88 88 89
③A、B两班学生测试成绩的平均数、中位数、方差如下：
平均数 | 中位数 | 方差 | |
A班 | 80.6 | m | 96.9 |
B班 | 80.8 | n | 153.3 |
根据以上信息，回答下列问题：
（1）补全数学成绩频数分布直方图；
（2）写出表中m、n的值；
（3）请你对比分析A、B两班学生的数学学习情况（至少从两个不同的角度分析）．
