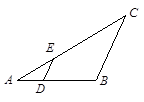题目内容
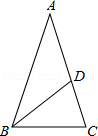
如图,在△ABC中,AB=AC,∠A=36°,BD平分∠ABC交AC于点D,若AC=2,则AD的长是( )


A. | B. | C.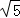 ﹣1 ﹣1 | D.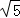 +1 +1 |
C
试题分析:根据两角对应相等,判定两个三角形相似.再用相似三角形对应边的比相等进行计算求出BD的长.
解:∵∠A=∠DBC=36°,∠C公共,
∴△ABC∽△BDC,
且AD=BD=BC.
设BD=x,则BC=x,CD=2﹣x.
由于
 =
= ,
,∴
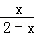 =
= .
.整理得:x2+2x﹣4=0,
解方程得:x=﹣1±
 ,
,∵x为正数,
∴x=﹣1+
 .
.故选C.
点评:本题考查的是相似三角形的判定与性质,先用两角对应相等判定两个三角形相似,再用相似三角形的性质对应边的比相等进行计算求出BD的长.

练习册系列答案
相关题目
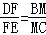 .
.


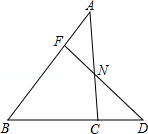
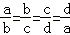 ,求
,求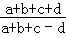 的值.
的值.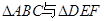 相似且对应高线的比为
相似且对应高线的比为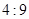 ,则
,则