题目内容
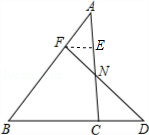
如图,已知点F在AB上,且AF:BF=1:2,点D是BC延长线上一点,BC:CD=2:1,连接FD与AC交于点N,求FN:ND的值.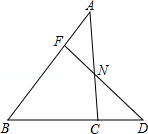

2:3
试题分析:过点F作FE∥BD,交AC于点E,求出
 =
= ,得出FE=
,得出FE= BC,根据已知推出CD=
BC,根据已知推出CD= BC,根据平行线分线段成比例定理推出
BC,根据平行线分线段成比例定理推出 =
=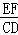 ,代入化简即可.
,代入化简即可.解:过点F作FE∥BD,交AC于点E,
∴
 =
= ,
,∵AF:BF=1:2,
∴
 =
= ,
,∴
 =
= ,
,即FE=
 BC,
BC,∵BC:CD=2:1,
∴CD=
 BC,
BC,∵FE∥BD,
∴
 =
= =
= =
= .
.即FN:ND=2:3.
证法二、连接CF、AD,

∵AF:BF=1:2,BC:CD=2:1,
∴
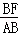 =
= =
= ,
,∵∠B=∠B,
∴△BCF∽△BDA,
∴
 =
= =
=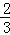 ,∠BCF=∠BDA,
,∠BCF=∠BDA,∴FC∥AD,
∴△CNF∽△AND,
∴
 =
= =
=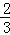 .
.
点评:本题考查了平行线分线段成比例定理的应用,注意:平行线分的线段对应成比例,此题具有一定的代表性,但是一定比较容易出错的题目.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
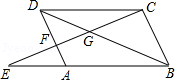

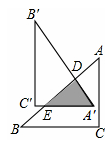
 =
=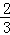 ,则四边形 ABCD ∽四边形 A′B′C′D′ ,且四边形ABCD与A′B′C′D′的相似比是 ,四边形ABCD与A′B′C′D′的面积比是 .
,则四边形 ABCD ∽四边形 A′B′C′D′ ,且四边形ABCD与A′B′C′D′的相似比是 ,四边形ABCD与A′B′C′D′的面积比是 .



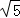 ﹣1
﹣1 ,则
,则 的值是( )
的值是( )