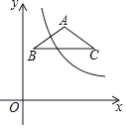题目内容
【题目】在△ABC中,∠BAC=45°,CD⊥AB于点D,AE⊥BC于点E,连接DE.
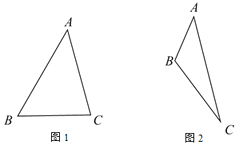
(1)如图1,当△ABC为锐角三角形时,
①依题意补全图形,猜想∠BAE与∠BCD之间的数量关系并证明;
②用等式表示线段AE,CE,DE的数量关系,并证明;
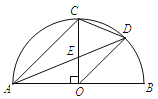
(2)如图2,当∠ABC为钝角时,依题意补全图形并直接写出线段AE,CE,DE的数量关系.
【答案】(1)①补全图形,如图1所示.见解析;猜想:∠BAE=∠BCD. 理由见解析;②见解析;(2)补全图形,如图3所示. 见解析;线段AE,CE,DE的数量关系:CE-![]() DE=AE.
DE=AE.
【解析】
(1)①依题意补全图形,由直角三角形的性质得出∠BAE﹢∠B=90°,
∠BCD﹢∠B=90°即可得出∠BAE=∠BCD;
②在AE上截取AF=CE,可证出△ACD是等腰直角三角形,得出AD=CD,可证明△ADF≌△CDE,得出DF=DE, ∠ADF=∠CDE,可推出∠CDE﹢∠FDC=∠EDF=90°.证出△EDF是等腰直角三角形,得出EF=![]() ,即可得出结论;
,即可得出结论;
(2) 在CE上截取CF=AE,连接DF由CD⊥AD,AE⊥BC,可得∠EAD=∠DCF
由∠BAC=45°可得AD=CD,可证△ADE≌△CDF,可得ED=DF∠ADE=∠CDF,可推出∠EDF=90°可得△EDF是等腰直角三角形故![]() ,即可得线段AE,CE,DE的数量关系.
,即可得线段AE,CE,DE的数量关系.
(1)①依题意,补全图形,如图1所示.
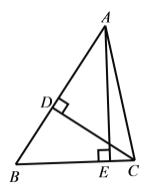
猜想:∠BAE=∠BCD.
理由如下:
∵CD⊥AB,AE⊥BC,
∴∠BAE﹢∠B=90°,
∠BCD﹢∠B=90°.
∴∠BAE=∠BCD.
②证明:如图2,在AE上截取AF=CE.
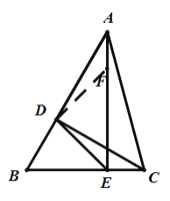
连接DF.
∵∠BAC=45°,CD⊥AB,
∴△ACD是等腰直角三角形.
∴AD=CD.
又∠BAE=∠BCD,
∴△ADF≌△CDE(SAS).
∴DF=DE, ∠ADF=∠CDE.
∵AB⊥CD,
∴∠ADF﹢∠FDC=90°.
∴∠CDE﹢∠FDC=∠EDF=90°.
∴△EDF是等腰直角三角形.
∴EF=![]() .
.
∵AF+EF=AE,
∴CE+![]() DE=AE.
DE=AE.
(2)依题意补全图形,如图3所示.

在CE上截取CF=AE,连接DF
∵CD⊥AD,AE⊥BC
∴∠ADC=∠AEC=90°
∴∠EAB+∠ABE=90°,∠DBC+∠DCF=90°,∠ABE=∠CBD
∴∠EAD=∠DCF
∵∠BAC=45°
∴∠DCA=45°
∴AD=CD
又∵CF=AE
∴△ADE≌△CDF
∴ED=DF
∠ADE=∠CDF
∵∠CDF+∠ADF=90°
∴∠ADE+∠ADF=90°
∴∠EDF=90°
∴△EDF是等腰直角三角形
∴![]()
∵CE=CF+EF
∴![]()
∴线段AE,CE,DE的数量关系:CE-![]() DE=AE.
DE=AE.
故答案为:CE-![]() DE=AE
DE=AE

 名校课堂系列答案
名校课堂系列答案