题目内容
【题目】已知二次函数y=﹣x2﹣2x+3
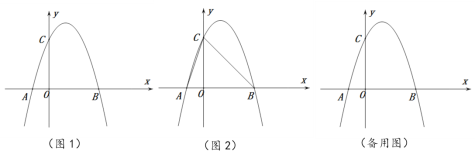
(1)求出顶点,并画出二次函数的图象.
(2)根据图象解决下列问题
①若y>0,写出x的取值范围.
②求出﹣![]() ≤x≤2时,y的最大值和最小值.
≤x≤2时,y的最大值和最小值.
③求出﹣5<y<3时,x的取值范围.
【答案】(1)(﹣1,4),见解析(2)①﹣3<x<1②4和﹣5③﹣4<x<﹣2或0<x<2
【解析】
(1)y=﹣x2﹣2x+3=﹣(x+1)2+4,即可求解;
(2)①若y>0,则﹣3<x<1;
②﹣![]() ≤x≤2时,y在顶点处取得最大值4,y在x=2时,取得最小值,当x=2时,y=﹣5,即可求解;
≤x≤2时,y在顶点处取得最大值4,y在x=2时,取得最小值,当x=2时,y=﹣5,即可求解;
③当y=﹣5时,即y=﹣x2﹣2x+3=﹣5,解得:x=2或﹣4,即可求解.
解:(1)y=﹣x2﹣2x+3=﹣(x+1)2+4,
顶点坐标为:(﹣1,4),
令y=0,则x=1或﹣3,令x=0,则y=3,
则函数图象如下:
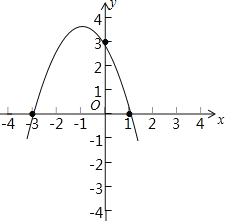
(2)①若y>0,则﹣3<x<1;
②﹣![]() ≤x≤2时,y在顶点处取得最大值4,
≤x≤2时,y在顶点处取得最大值4,
y在x=2时,取得最小值,当x=2时,y=﹣5,
故y的最大值和最小值分别为:4和﹣5;
③当y=﹣5时,即y=﹣x2﹣2x+3=﹣5,解得:x=2或﹣4,
当y=3时,同理x=0或﹣2,
从图象看:﹣5<y<3时,﹣4<x<﹣2或0<x<2.

练习册系列答案
 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目