题目内容
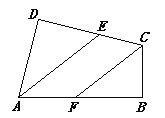
【题目】如图,在四边形ABCD中, ∠B=∠D=90°,∠DAB与∠DCB 的平分线分别交DC,AB于E,F.求证:AE∥CF.
【答案】证明见解析.
【解析】试题分析:
由四边形内角和为360°及∠B=∠D=90°,易得∠DAB+∠BCD=180°,∠BFC+∠BCF=90°,再由AE,CF分别平分∠DAB与∠DCB可得∠EAB+∠BFC=90°,从而可得∠EAB=∠BFC,就可证得AE∥CF.
试题解析:
∵∠DAB+∠B+∠BCD+∠D=360°,∠B=∠D=90°,
∴∠DAB+∠BCD=360°-∠B-∠D=180°,∠BFC+∠BCF=90°.
∵AE,CF分别平分∠DAB与∠DCB,
∴![]() ,
, ![]() .
.
∴![]()
∴∠EAB=∠BFC.
∴AE∥CF.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目