题目内容
【题目】已知抛物线y=ax2+bx+c的顶点为(1,0),且经过点(0,1).
(1)求该抛物线对应的函数的解析式;
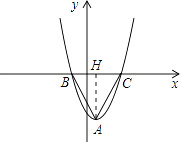
(2)将该抛物线向下平移m(m>0)个单位,设得到的抛物线的顶点为A,与x轴的两个交点为B、C,若△ABC为等边三角形.
①求m的值;
②设点A关于x轴的对称点为点D,在抛物线上是否存在点P,使四边形CBDP为菱形?若存在,写出点P的坐标;若不存在,请说明理由.
【答案】
(1)
解:由题意可得, 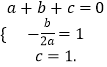 ,解得
,解得 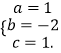 ,
,
故抛物线对应的函数的解析式为y=x2﹣2x+1
(2)
解:①将y=x2﹣2x+1向下平移m个单位得:y=x2﹣2x+1﹣m=(x﹣1)2﹣m,
令y=x2﹣2x+1﹣m=(x﹣1)2﹣m=0,
解得x=1﹣ ![]() 或x=1+
或x=1+ ![]() ,
,
可知A(1,﹣m),B(1﹣ ![]() ,0),C(1+
,0),C(1+ ![]() ,0),BC=2
,0),BC=2 ![]() ,
,
过点A作AH⊥BC于H,
∵△ABC为等边三角形,
∴BH=HC= ![]() BC,∠CAH=30°,
BC,∠CAH=30°,
∴AH= ![]() ,即
,即 ![]() =m,
=m,
由m>0,解得m=3.
②在抛物线上存在点P,能使四边形CBDP为菱形.理由如下:
∵点D与点A关于x轴对称,
∴D(1,3),
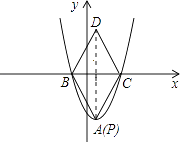
①当DP为对角线时,显然点P在点A位置上时,符合题意,
故此时点P坐标为(1,﹣3);
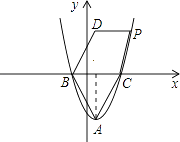
②当DP为边时,要使四边形CBDP为菱形,需DP∥BC,DP=BC.
由点D的坐标为(1,3),DP=BC=2 ![]() ,可知点P的横坐标为1+2
,可知点P的横坐标为1+2 ![]() ,
,
当x=1+2 ![]() 时,y=x2﹣2x+1﹣m=x2﹣2x﹣2=
时,y=x2﹣2x+1﹣m=x2﹣2x﹣2= ![]() ﹣2(1+2
﹣2(1+2 ![]() )﹣2=11≠3,
)﹣2=11≠3,
故不存在这样的点P.
综上可得,存在使四边形CBDP为菱形的点P,坐标为(1,﹣3).
【解析】(1)根据抛物线的顶点坐标及函数经过点(0,1),利用待定系数法求解即可.(2)①先写出平移后的函数解析式,然后得出A、B、C三点的坐标,过点A作AH⊥BC于H,根据△ABC为等边三角形,可得出关于m的方程,解出即可;②求出点D坐标,分两种情况进行讨论,①PD为对角线,②PD为边,根据菱形的性质求解即可.
【考点精析】认真审题,首先需要了解二次函数的性质(增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小).