题目内容
【题目】对于平面直角坐标系![]() 内任意一点P,过P点作
内任意一点P,过P点作![]() 轴于点M,
轴于点M,![]() 轴于点N,连接
轴于点N,连接![]() ,则称
,则称![]() 的长度为点P的垂点距离,记为h.特别地,点P与原点重合时,垂点距离为0.
的长度为点P的垂点距离,记为h.特别地,点P与原点重合时,垂点距离为0.
(1)点![]() 的垂点距离分别为________,___________,____________;
的垂点距离分别为________,___________,____________;
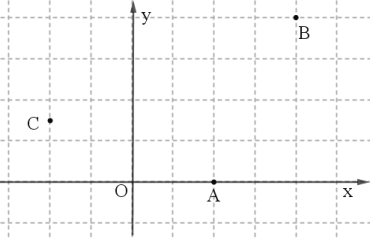
(2)点P在以![]() 为圆心,半径为3的
为圆心,半径为3的![]() 上运动,求出点P的垂点距离h的取值范围;
上运动,求出点P的垂点距离h的取值范围;
(3)点T为直线![]() 位于第二象限内的一点,对于点T的垂点距离h的每个值有且仅有一个点T与之对应,求点T的横坐标t的取值范围.
位于第二象限内的一点,对于点T的垂点距离h的每个值有且仅有一个点T与之对应,求点T的横坐标t的取值范围.
【答案】(1)![]() ;(2)1≤
;(2)1≤![]() ≤ 5;(3)
≤ 5;(3)![]() 或
或![]()
【解析】
(1)运用勾股定理计算出三点的垂点距离;
(2)过点P作![]() 轴于点M,
轴于点M,![]() 轴于点N,易证四边形
轴于点N,易证四边形![]() 是矩形,所以OP=MN,则求点P的垂点距离h的取值范围,及求圆上一点P到坐标圆点O的取值范围;
是矩形,所以OP=MN,则求点P的垂点距离h的取值范围,及求圆上一点P到坐标圆点O的取值范围;
(3)设直线l与x轴,y轴的交点分别为![]() ,过点O作
,过点O作![]() 直线l于点M,以
直线l于点M,以![]() 为半径作
为半径作![]() ,交直线l于点N,过点
,交直线l于点N,过点![]() 分别作x轴的垂线,垂足分别为
分别作x轴的垂线,垂足分别为![]() ,求出OC,OD的距里,从而找到t的取值范围.
,求出OC,OD的距里,从而找到t的取值范围.
解:(1)如图所示:
∴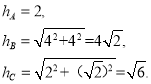 .
.

(2)如图,过点P作![]() 轴于点M,
轴于点M,![]() 轴于点N.
轴于点N.

![]() ,
,
![]() 四边形
四边形![]() 是矩形.
是矩形.
![]() .
.
![]() 点坐标为
点坐标为![]() ,
,
![]() .
.
![]() ,
,
![]() .
.
![]() .
.
(3)如图,设直线l与x轴,y轴的交点分别为![]() ,过点O作
,过点O作![]() 直线l于点M,以
直线l于点M,以![]() 为半径作
为半径作![]() ,交直线l于点N.
,交直线l于点N.

![]() ,
,
![]() .
.
过点![]() 分别作x轴的垂线,垂足分别为
分别作x轴的垂线,垂足分别为![]() ,
,
则![]() ,即
,即![]() .
.
![]() 是等边三角形,
是等边三角形,
![]() .
.
![]() 或
或![]() .
.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目