Question

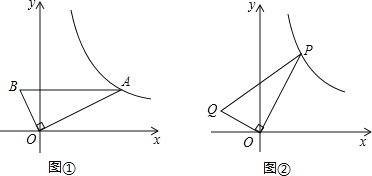
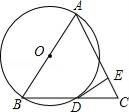
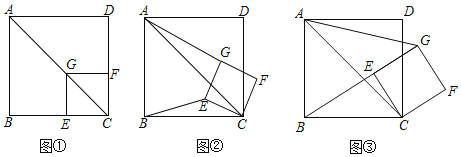
【题目】如图(1)，将正方形ABCD与正方形GECF的顶点C重合，当正方形GECF的顶点G在正方形ABCD的对角线AC上时，的值为______.

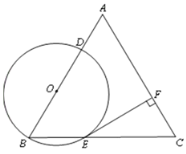
如图(2)，将正方形CEGF绕点C顺时针方向旋转a角(0°＜a＜45°)，猜测AG与BE之间的数量关系，并说明理由.

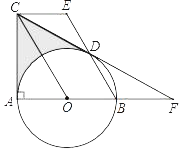
如图(3)，将正方形CEGF绕点C顺时针方向旋转a角(45°＜a＜90°)使得B、E、G三点在一条直线上，此时tan∠GAC＝，AG＝6，求△BCE的面积.

Answer 1

【答案】(1)；(2)＝，理由见解析；(3)3.

【解析】

(1)根据AC＝BC，CG＝EC，可得AG＝BE，即＝.

(2)根据△BCE∽△AGC，利用对应边之间的比例关系就可以得到AG和BE的比值.

(3)利用相似三角形的性质证明∠AGC＝90°，求出BE，EC即可解决问题.

(1)如图1中，

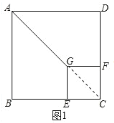
∵四边形CEGF是正方形，

∴∠CEG=90°，∠ECG=45°，=，

∵四边形ABCD是正方形，

∴∠B=90°,∠BCA=45°，

∴A，G，C三点在一条直线上，

∵∠CEG=90°，∠B=90°，

∴GE∥AB，

∴，

∴＝，

故答案为：.

(2)结论：＝.

如图②中，所示，连接CG.

∵∠ECG=∠BCA=45°，

∴∠BCE=∠ACG=45°∠ACE，

在Rt△CEG和Rt△CBA中，

CG=CE，CA=CB，

∴，

∴△ACG∽△BCE，

∴＝，

∴＝.

(3)如图③中，连接CG，、

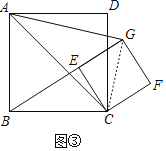
∵∠ACG＝∠BCE，＝，

∴△ACG∽△BCE，

∴∠GAC＝∠EBC，∠AGC＝∠BEC＝90°，

∵AG＝6，

∴BE＝3，

∵tan∠EBC＝tan∠GAC＝，

∴∠EBC＝30°，

在Rt△BEC中，tan∠EBC＝，

∴EC＝，

∴S△BEC＝BEEC＝×3×＝3.