Question

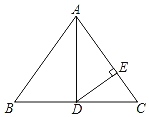
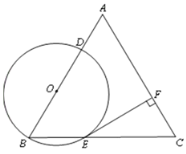
【题目】已知：△ABC是边长为4的等边三角形，点O在边AB上，⊙O过点B且

分别与边AB，BC相交于点D，E，EF⊥AC，垂足为F.

（1）求证：直线EF是⊙O的切线；

（2）当直线DF与⊙O相切时，求⊙O的半径.

Answer 1

【答案】（1）见解析；（2）⊙O的半径是．

【解析】

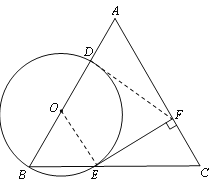
（1）证明：连接OE，则OB=OE．

∵△ABC是等边三角形， ∴∠ABC=∠C=60°.

∴△OBE是等边三角形.

∴∠OEB=∠C=60°.

∴OE∥AC．

∵EF⊥AC，∴∠EFC=90°．

∴∠OEF=∠EFC=90°．

∴EF是⊙O的切线；

（2）连接DF,

∵DF是⊙O的切线， ∴∠ADF=90°．

设⊙O的半径为r，则BE=r，EC=，AD=．

在Rt△ADF中，∵∠A=60°， ∴AF=2AD=．

∴FC=．

在Rt△CEF中 ，∵∠C=60°， ∴EC=2FC，

∴=2（），

解得，

∴⊙O的半径是．