题目内容
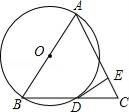
【题目】如图,△ABC 中,AB=AC,以AB为直径作⊙O,与BC交于点D,过D作AC的垂线,垂足为E.
证明:(1)BD=DC;(2)DE是⊙O切线.
【答案】详见解析
【解析】
试题分析:(1)连接AD,由于AB是直径,那么∠ADB=90°,而AB=AC,根据等腰三角形三线合一定理可知BD=CD;
(2)连接OD,由于∠BAC=2∠BAD,∠BOD=2∠BAD,那么∠BAC=∠BOD,可得OD∥AC,而DE⊥AC,易证∠ODB=90°,从而可证DE是⊙O切线.
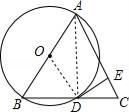
试题解析:如右图所示,
(1)连接AD,∵AB是直径,∴∠ADB=90°,又∵AB=AC,∴BD=CD;
(2)连接OD,∵∠BAC=2∠BAD,∠BOD=2∠BAD,∴∠BAC=∠BOD,∴OD∥AC,
又∵DE⊥AC,∴∠AED=90°,∴∠ODB=∠AED=90°,∴DE是⊙O的切线.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案
相关题目