Question

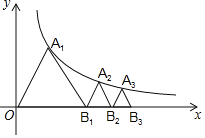
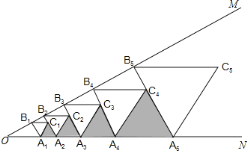
【题目】如图，∠MON＝30°，点B1在边OM上，且OB1＝3，过点B1作B1A1⊥OM交ON于点A1，以A1B1为边在A1B1右侧作等边三角形A1B1C1；过点C1作OM的垂线分别交OM、ON于点B2、A2，以A2B2为边在A2B2的右侧作等边三角形A2B2C2；过点C2作OM的垂线分别交OM、ON于点B3、A3，以A3B3为边在A3B3的右侧作等边三角形A3B3C3，…；按此规律进行下去，则△An﹣1AnCn﹣1的高为______.(用含正整数n的代数式表示)

Answer 1

【答案】()n﹣1

【解析】

证明△A1A2C1是等边三角形，△A2A3C2、…、△An﹣1AnCn﹣1都是等边三角形，求出A1C1＝A1B1＝B1C1＝，由等边三角形的性质得出等边△A1A2C1的高为：A1C1＝，同理求出等边△A2A3C2的高为：A2C2＝()2，…，得出规律即可；

解：∵∠MON＝30°，B1A1⊥OM，△A1B1C1是等边三角形，

∴A1B1＝OB1＝，

∠OA1B1＝60°，∠B1A1C1＝60°，

∴∠C1A1A2＝60°，

∵A2B2⊥OM，

∴A2B2∥A1B1，

∴∠A1A2C1＝∠OA1B1＝60°，

∴△A1A2C1是等边三角形，

同理：△A2A3C2、…、△An﹣1AnCn﹣1都是等边三角形，

∴A1C1＝A1B1＝B1C1＝，

∴等边△A1A2C1的高为：A1C1＝，

∵∠C1B1B2＝90°﹣60°＝30°，

∴B2C1＝B1C1＝，

∴A2C2＝A2B2＝A1C1+B2C1＝，

∴等边△A2A3C2的高为：A2C2＝×＝()2，…，

∴△An﹣1AnCn﹣1的高为()n﹣1；

故答案为：()n﹣1.