��Ŀ����
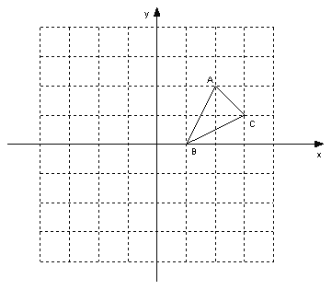
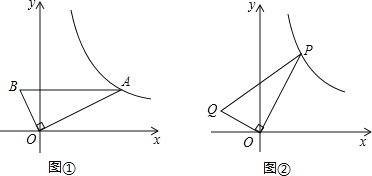
����Ŀ����ͼ�٣�ֱ��������AOB�У���AOB=90����ABƽ����x�ᣬOA=2OB��AB=5��������������ͼ����A��
��1��ֱ��д�������������Ľ���ʽ��
��2����ͼ�ڣ�P��x��y���ڣ�1���еķ���������ͼ���ϣ�����1��x��8������OP����O ��OQ��OP����OP=2OQ������PQ����Q����Ϊ��m��n��������m��0��n��0����n��m�ĺ�������ʽ����ֱ��д���Ա���m��ȡֵ��Χ��
��3���ڣ�2���������£���Q����Ϊ��m��1��������POQ�������
���𰸡���1��y=![]() ����2��n=
����2��n=![]() ����4��m����
����4��m����![]() ������3��5.
������3��5.
��������
��1����ͼ�٣�
�ߡ�AOB=90����
��OA2+OB2=AB2��
��OA=2OB��AB=5��
��4OB2+OB2=25�����OB=![]() ��
��
��OA=2![]() ��
��
��ABƽ����x�ᣬ
��OC��AB��
��![]() OCAB=
OCAB=![]() OBOA����OC=
OBOA����OC=![]() =2��
=2��
��Rt��AOC��AC=4��
��A��������4��2����
���A��ķ�������������ʽΪy=![]() ��
��
��k=4��2=8��
�෴������������ʽΪy=![]() ��
��
��2���ֱ��P��Q��x�ᴹ�ߣ�����ֱ�ΪD��H����ͼ�ڣ�
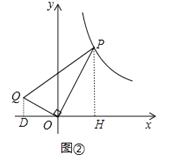
��OQ��OP��
���POH+��QOD=90����
�ߡ�POH+��OPH=90����
���QOD=��OPH��
��Rt��POH��Rt��OQD��
��![]() ��
��
��P��x��y���ڣ�1���еķ���������ͼ���ϣ�����1��x��8��Q������Ϊ��m��n��������m��0��n��0��OP=2OQ��
��PH=y��OH=x��OD=��m��QD=n��
��![]() �����x=2n��y=��2m��
�����x=2n��y=��2m��
��y=![]() ��
��
��2n����2m��=8��
��mn=��2����4��m����![]() ����
����
��n=![]() ����4��m����
����4��m����![]() ����
����
��3����n=1ʱ��m=��2����Q������Ϊ����2��1����
��OQ=![]() ��
��
��OP=2OQ=![]() ��
��
��S��POQ=![]() ��
��