Question

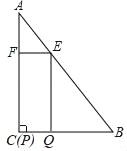
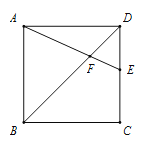
【题目】如图，在正方形ABCD中，点E在边CD上(不与点C，D重合)，连接AE，BD交于点F.

（1）若点E为CD中点，AB＝2，求AF的长.

（2）若∠AFB＝2，求的值.

（3）若点G在线段BF上，且GF＝2BG，连接AG，CG，设＝x，四边形AGCE的面积为，ABG的面积为，求的最大值.

Answer 1

【答案】（1）；（2）；（3）.

【解析】

（1）由可得DE的长，利用勾股定理可得AE的长，又易证，由相似三角形的性质可得，求解即可得；

（2）如图（见解析），连接AC与BD交于点O，由正方形的性质可知，，，设，在中，可求出，从而可得DF和BF的长，即可得出答案；

（3）设正方形的边长，可得DE、AO、BO、BD的长，由可得BF的长，又根据可得BG的长，从而可得的面积，用正方形的面积减去三个三角形的面积可得四边形AGCE的面积，再利用二次函数的性质求解的最大值.

（1）为CD中点，

，

，即

又

；

（2）如图，连接AC与BD交于点O

由正方形的性质得，

设

在中，

，

；

（3）设正方形的边长，则

由（1）知，

又

又

又

由二次函数图象的性质得：当时，有最大值，最大值为.