��Ŀ����
����Ŀ���Ķ����ϣ�������⣺
����1�����о���������ʱ���֣��ܱ�5��25��125��625���������������ǣ��ֱ��������ĩһλ��ĩ��λ��ĩ��λ��ĩ��λ���ɣ��ƹ��һ�����ۣ�ĩ![]() λ�ܱ�
λ�ܱ�![]() �����������������ܱ�
�����������������ܱ�![]() ��������������ĩ
��������������ĩ![]() λ���ܱ�
λ���ܱ�![]() ��������������Ҳ�����ܱ�
��������������Ҳ�����ܱ�![]() �����������ж�992250�ܷ�25��625����ʱ���ɰ����в�����㣺
�����������ж�992250�ܷ�25��625����ʱ���ɰ����в�����㣺
![]() ��
��![]() ������
Ϊ������![]() �ܱ�25����
�ܱ�25����
![]() ��
��![]() ��������
��Ϊ������![]() ���ܱ�625����
���ܱ�625����
����2������żλ��ж�һ�����ܷ�11���������ʱ���ɰ����������λ�ϵ�������żλ�ϵ����ֱַ���������������ǵIJ�����ܷ�11�����������ܱ�11��������ԭ���ܱ�11��������֮����.
��1����![]() �����λ���ܱ�11��������
�����λ���ܱ�11��������![]() �������ڸ���λ��ĩβ���Ϻ�Ϊ8���������֣������Ϊһ����λ��������λ�����ܱ�11�������������λ��
�������ڸ���λ��ĩβ���Ϻ�Ϊ8���������֣������Ϊһ����λ��������λ�����ܱ�11�������������λ��
��2����һ����λ��p�����λ����Ϊ5��ǧλ�����Ǹ�λ���ֵ�2��������������ܱ�125���������ܱ�11���������������
���𰸡���1��m��8��68244����2�������Ϊ580250��500500��530750��550000.
��������
��1������λ�ֱ���6��2��ż��Ϊ��m�����������֪6��2m�ܱ�11��������mΪ0��9�������Ӷ������m��ֵ�������λ��Ϊ![]() ���������֪a��b��8������ba��11n���Ӷ����a��b��ֵ��
���������֪a��b��8������ba��11n���Ӷ����a��b��ֵ��
��2���������λ��pΪ![]() �����������֪��b��2e������eֻ��ȡ0��1��2��3��4���ɲ���һ��֪��
�����������֪��b��2e������eֻ��ȡ0��1��2��3��4���ɲ���һ��֪��![]() �ܱ�125��������֪
�ܱ�125��������֪![]() ��250��500��750��Ȼ���������a��b��c��d��e��ֵ��
��250��500��750��Ȼ���������a��b��c��d��e��ֵ��
�⣺��1������λ�ֱ���6��2��ż��Ϊ��m��
���ɲ��Ͽ�֪��6��2m�ܱ�11������
��0��m��9����m����������
��m��8��
�����λ��Ϊ![]() ��
��
������λ֮��Ϊ��b+2+6��ż��λ֮��Ϊ��a��8��
����������֪��8��b8a��ba�ܱ�11������
����ba��11n��n������
��a��b��8��
��![]() ��
��
���ã�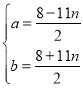 ��
��
��0��a��9��0��b��9��
��![]() ��
��![]() ��
��
��![]() ��
��
��n��0��
��a��4��b��4��
�����Ϊ68244��
��2���������λ��pΪ![]() ��
��
�������֪��b��2e��
��0��b��9��
��0��e��4.5��
��e��0��1��2��3��4��
��![]() �ܱ�125������
�ܱ�125������
��![]() ��125n��n��������
��125n��n��������
��1��n��7��
��e��0��1��2��3��4��
��n��2��4��6��
��![]() ��250��500��750��000
��250��500��750��000
��ż��λ֮��Ϊ��5��b��d��5��2e��d������λ֮��Ϊ��a��c��e��
��|��5��2e��d����a��c��e��|��|5��e��dac|�ܱ�11������
��![]() ��250ʱ��
��250ʱ��
��c��2��d��5��e��0��b��0��
��|5��e��dac|��|8a|��
��|8a|��11m��m��������
��a��8��11m��
��0��a��9��
��![]() ��m��
��m��![]() ��
��![]() ��m��
��m��![]() ��
��
��m��0
��a��8��
�����Ϊ580250��
ͬ������![]() ��500ʱ������Ϊ500500��
��500ʱ������Ϊ500500��
��![]() ��750ʱ������Ϊ530750��
��750ʱ������Ϊ530750��
��![]() ��000ʱ������Ϊ550000
��000ʱ������Ϊ550000
��������������Ϊ580250��500500��530750��550000.

 �Ǽ�����������ϵ�д�
�Ǽ�����������ϵ�д� â���̸������Ծ�ϵ�д�
â���̸������Ծ�ϵ�д�����Ŀ��ij��ͯ������Ʊ�۸�涨���±���
��Ʊ���� | 1~50�� | 51~100�� | 100������ |
ÿ��Ʊ�ļ۸� | 13Ԫ | 11Ԫ | 9Ԫ |
ijУ���꼶��1������2�������102�˽���6��1��ͯ��ȥ�θ����������У�1�����������٣�����50�ˣ������㣬����������Ϊ��λ��Ʊ����һ��Ӧ��1218Ԫ���ʣ�
��1����������ж���ѧ����
��2���������������������Ϊһ�����幺Ʊ�����Խ�ʡ����Ǯ��
��3��������꼶��1������10��ѧ����ѧУ�������ܲμ�������Σ�����Ϊ��������Ƴ�������Ʊ�ķ�������ָ����ʡǮ�ķ�����
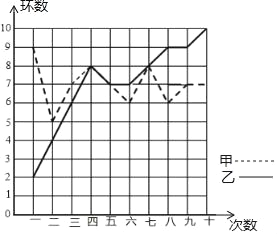
����Ŀ��ij������Ӽס���������Ա����ͬ�������¸����10�Σ�ÿ����ҵijɼ������ͼ��ʾ��
��1���뽫�±��������������ο���ʽ������S2=![]() [��x1��
[��x1��![]() ��2+��x2��
��2+��x2��![]() ��2+��+��xn��
��2+��+��xn��![]() ��2]��
��2]��
ƽ���� | ���� | ��λ�� | |
�� | 7 | �� �� | 7 |
�� | �� �� | 5.4 | �� �� |
��2���������������ͬ�ĽǶȶ���β��Խ������
�ٴ�ƽ�����ͷ������Ͽ����� ���ijɼ���Щ��
�ڴ�ƽ��������λ�����Ͽ����� ���ijɼ���Щ��
����������ѡ����óɼ���9�����ң���Ҫѡһ�˲���������Ϊѡ˭�μӣ���˵�����ɣ�