Question

【题目】已知二次函数y= x2－4x＋3．

（1）把这个二次函数化成的形式并写出抛物线的顶点坐标；

（2）画出这个二次函数的图象，并利用图象直接写出当y>0时，x的取值范围． 当x取何值时，y随x的增大而减小；

（3）若抛物线与轴的交点记为A，B，该图象上存在一点C，且△ABC的面积为3，求点C的坐标．

Answer 1

【答案】（1） -1，（2，-1）；（2），； ；（3）（4，3），（0，3）

【解析】

（1）利用配方法先提出二次项系数，再加上一次项系数的一半的平方来凑完全平方式，把一般式转化为顶点式，根据顶点式即可求得顶点坐标．

（2）根据顶点坐标，抛物线与y轴的交点坐标以及抛物线与x轴的交点坐标画出图象，根据图象求得当y＞0时，x的取值范围，当x＜2，y随x的增大而减小；

（3）S△ABC＝×AB×yC即可求解．

（1）y＝x24x＋3＝（x2）21，则该抛物线解析式是y＝（x2）21；

∴抛物线的顶点为（2，1）；

（2）画出函数图象如图：

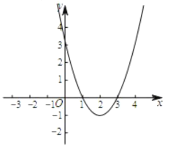
当y＞0时，x的取值范围是x＜1或x＞3．当x＜2，y随x的增大而减小；

（3）由图可知：A（1，0），B（3，0）

∴AB=2

∵S△ABC＝×AB×yC＝×2×3＝3．

∴yC=3，故x24x＋3＝3，

解得x1=0,x2=4，

故C点（4，3），（0，3）.