题目内容
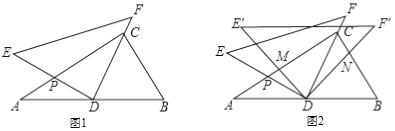
【题目】已知△ABC中,AB=AC,点P是AB上一动点,点Q是AC的延长线上一动点,且点P从B运动向A、点Q从C运动向Q移动的时间和速度相同,PQ与BC相交于点D,若AB=![]() ,BC=16.
,BC=16.
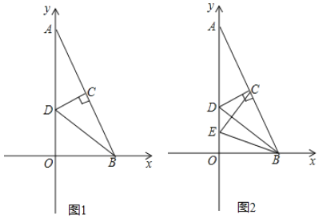
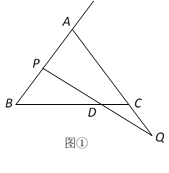
(1)如图1,当点P为AB的中点时,求CD的长;
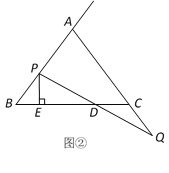
(2)如图②,过点P作直线BC的垂线,垂足为E,当点P、Q在移动的过程中,设BE+CD=λ,λ是否为常数?若是请求出λ的值,若不是请说明理由.
【答案】(1)4;(2)8
【解析】
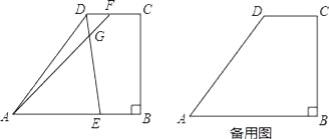
(1)过P点作PF∥AC交BC于F,由点P和点Q同时出发,且速度相同,得出BP=CQ,根据PF∥AQ,可知∠PFB=∠ACB,∠DPF=∠CQD,则可得出∠B=∠PFB,证出BP=PF,得出PF=CQ,由AAS证明△PFD≌△QCD,得出,再证出F是BC的中点,即可得出结果;
(2)过点P作PF∥AC交BC于F,易知△PBF为等腰三角形,可得BE=![]() BF,由(1)证明方法可得△PFD≌△QCD 则有CD=
BF,由(1)证明方法可得△PFD≌△QCD 则有CD=![]() ,即可得出BE+CD=8.
,即可得出BE+CD=8.
解:(1)如图①,过P点作PF∥AC交BC于F,
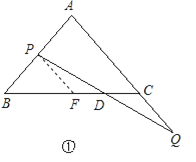
∵点P和点Q同时出发,且速度相同,
∴BP=CQ,
∵PF∥AQ,
∴∠PFB=∠ACB,∠DPF=∠CQD,
又∵AB=AC,
∴∠B=∠ACB,
∴∠B=∠PFB,
∴BP=PF,
∴PF=CQ,又∠PDF=∠QDC,
∴△PFD≌△QCD,
∴DF=CD=![]() CF,
CF,
又因P是AB的中点,PF∥AQ,
∴F是BC的中点,即FC=![]() BC=8,
BC=8,
∴CD=![]() CF=4;
CF=4;
(2)![]() 为定值.
为定值.
如图②,点P在线段AB上,
过点P作PF∥AC交BC于F,

易知△PBF为等腰三角形,
∵PE⊥BF
∴BE=![]() BF
BF
∵易得△PFD≌△QCD
∴CD=![]()
∴![]()

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目