题目内容
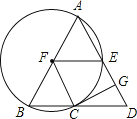
【题目】如图,在![]() 中,
中,![]() ,以AB为直径的
,以AB为直径的![]() 交BD于点C,交AD于点E,
交BD于点C,交AD于点E,![]() 于点G,连接FE,FC.
于点G,连接FE,FC.
![]() 求证:GC是
求证:GC是![]() 的切线;
的切线;
![]() 填空:
填空:
![]() 若
若![]() ,
,![]() ,则
,则![]() 的面积为______.
的面积为______.
![]() 当
当![]() 的度数为______时,四边形EFCD是菱形.
的度数为______时,四边形EFCD是菱形.
【答案】![]()
![]()
【解析】
(1)由等腰三角形的性质得出∠D=∠BCF,证出CF∥AD,由已知条件得出CG⊥CF,即可得出结论;
(2)解:①连接AC,BE,根据圆周角定理得到AC⊥BD,∠AEB=90°,根据等腰三角形的性质得到BC=CD,解直角三角形得到DE=2![]() -2,根据三角形的中位线的性质得到DG=EG=
-2,根据三角形的中位线的性质得到DG=EG=![]() DE=
DE=![]() -1,CG=
-1,CG=![]() BE=1,于是得到结论;
BE=1,于是得到结论;
②证出△BCF是等边三角形,得出∠B=60°,CF=BF=![]() AB,证出△ABD是等边三角形,CF=
AB,证出△ABD是等边三角形,CF=![]() AD,证出△AEF是等边三角形,得出AE=AF=
AD,证出△AEF是等边三角形,得出AE=AF=![]() AB=
AB=![]() AD,因此CF=DE,证出四边形EFCD是平行四边形,即可得出结论.
AD,因此CF=DE,证出四边形EFCD是平行四边形,即可得出结论.
![]() 证明:
证明:![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 是
是![]() 的切线;
的切线;
![]() 解:
解:![]() 连接AC,BE,
连接AC,BE,
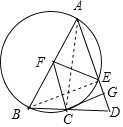
![]() 是
是![]() 的直径,
的直径,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() 的面积
的面积![]() ;
;
故答案为:![]() ;
;
![]() 当
当![]() 的度数为
的度数为![]() 时,四边形EFCD是菱形
时,四边形EFCD是菱形![]() 理由如下:
理由如下:
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() 是等边三角形,
是等边三角形,
![]() ,
,![]() ,
,
![]() ,
,
![]() 是等边三角形,
是等边三角形,![]() ,
,
![]() ,
,
![]() ,
,
![]() 是等边三角形,
是等边三角形,
![]() ,
,
![]() ,
,
又![]() ,
,
![]() 四边形EFCD是平行四边形,
四边形EFCD是平行四边形,
![]() ,
,
![]() 四边形EFCD是菱形;
四边形EFCD是菱形;
故答案为:![]() .
.

【题目】某厂工人小王某月工作的部分信息如下:
信息一:工作时间:每天上午![]() ,下午
,下午![]() ,每月
,每月![]() 天;
天;
信息二:生产甲、乙两种产品,并且按规定每月生产甲产品的件数不少于![]() 件.
件.
生产产品件数与所用时间之间的关系见下表:
生产甲产品数(件) | 生产乙产品数(件) | 所用时间 (分) |
|
|
|
|
|
|
信息三:按件计酬:每生产一件甲产品可得![]() 元,每生产一件乙产品可得
元,每生产一件乙产品可得![]() 元.
元.
根据以上信息,回答下列问题:
(1)小王每生产一件甲种产品,每生产一件乙种产品分别需要多少分钟;
(2)小王该月最多能得多少元,此时生产甲、乙两种产品分别多少件.